注意力机制

什么是注意力

首先，心理学上，作为动物，想要在复杂环境下关注到需要关注的事物，机制是根据随意线索和不随意线索选择注意点

随意与不随意实际上是遂意与不遂意，也就是是否受控

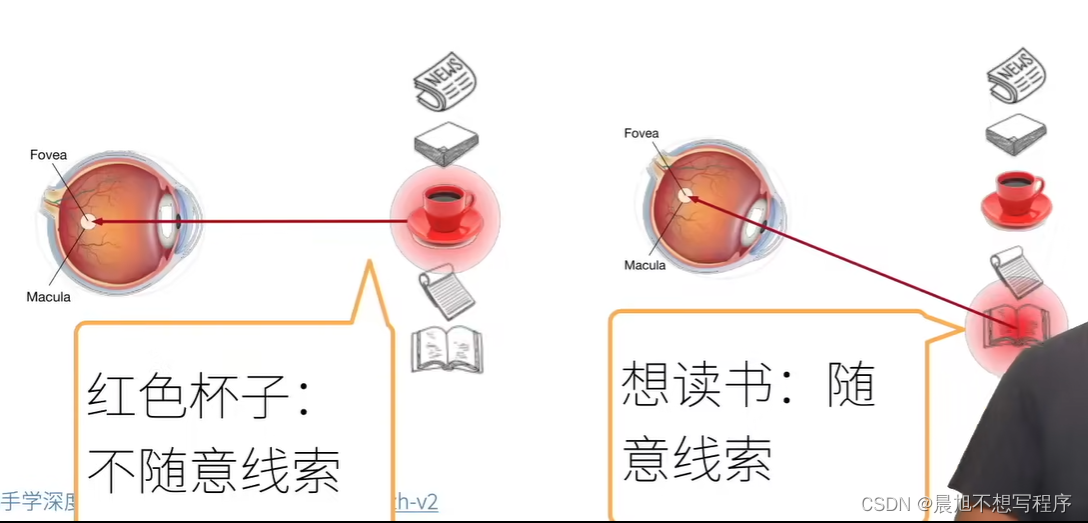
例如这里的在环境中看到红色杯子，是因为杯子颜色鲜艳，会让人第一眼看到，这是不需要遂意的，而想读书带着个人意愿，是遂意的在搜索

注意力机制

像之前学习过的卷积 全连接 池化层 都是只考虑不随意线索，更倾向于关注有特点的事物

注意力机制则显示的考虑随意线索

• 随意线索被称之为查询(query) ——》要求，想法
• 每个输入是一个值(value)和不随意线索(key)的对 ——》 环境，也就是存放一堆事物的场景
• 通过注意力池化层来有偏向性的选择选择某些输入 ——》 根据想法，根据在环境中为事物的不同价值选择观察事物

查询，键和值

在此之前提出QKV的概念

所谓Q即为query，被称为查询，即自主性提示，给定任何查询，注意力机制通过注意力汇聚将选择引导至感官输入，这些感官输入被称为V，即value，每个值都与一个键K，即key匹配，可以想象为非自主性提示。

非参注意力汇聚

$$ f(x)=\sum_{i=1}^{n}{\frac{K(x-x_{i})}{\sum_{i=1}^{n}{K(x-x_{j})}}}y_{i} $$

其中$K()$的作用就是衡量$X$与$X_i$之间关系的一个函数

$X$就是所谓的Q，是自主性提示

而$X_i$是所谓的K,与V一一对应，是非自主性提示

而他们的差值最小二乘，衡量他们的关系，此时二者差距越小，越接近，则此$y_i$所对应的权重就越大，即注意力分配越多，由此就得到了对应的汇聚函数

$$ K(u)=\frac{1}{\sqrt{2\pi}}\,\mathrm{Exp}(-\frac{u^{2}}{2}) $$

$$ \begin{array}{c}{{f(x)=\sum_{i=1}^{n}\frac{\exp\left(-\frac{1}{2}(x-x_{i})^{2}\right)}{\sum_{j=1}^{n}\exp\left(-\frac{1}{2}(x-x_{j})^{2}\right)}y_{i}}}\\ {{\displaystyle=\sum_{i=1}^{n}\mathrm{softmax}\left(-\frac{1}{2}(x-x_{i})^{2}\right)y_{i}}}\end{array} $$

这里实际上就是做了一个softmax操作

有参注意力汇聚

在此基础上引入可以学习的$w$ ,就实现了有参数的注意力汇聚

f(x)= $ \sum _ {i=1}^ {n} $ soft $ \max $ (- $ \frac {1}{2} $ $ ((x-x_ {i})w)^ {2} $

注意力评分

上文所示高斯核其实就是注意力评分函数，进行运算后得到与键对应的值的概率分布，即注意力权重

加性注意力

一般来说，当查询和键是不同长度的向量时，可以使用加性注意力作为评分函数

k $ \in $ $ R^ {h\times k} $ , $ W_ {q} $ $ \in $ $ R^ {h\times q} $ ,v $ \in $ $ R^ {h} $
a(k,q)= $ v^ {T} $ $ \tanh $ ( $ W_ {k} $ k+ $ W_ {q} $ q)

等价于将key与value合并起来后放入到一个隐藏大小为$h$，输出大小为1的单隐藏层MLP

缩放点积注意力

直接使用点积可以得到计算效率很高的评分函数，但是点积操作需要K与Q拥有相同的长度d，此时如果将

a(q, $ k_ {i} $ )= $ \langle $ q, $ k_ {i} $ $\rangle$ /$\sqrt {d} $

除一个根号d的目的是为了消除长度的影响

使用注意力机制的seq2seq

之前提到使用两个循环神经网络的编码器解码器结构实现了seq2seq的学习，实现 机器翻译的功能

循环神经网络编码器将可变序列转换为固定形状的上下文变量，然后循环神经网络解码器根据生成的词元和上下文变量按词元生成输出序列词元

然而不是所有的输入词元 都对 解码某个词元 都有用，在每个解码步骤中仍使用编码相同的上下文变量

在此时attention的加入就能改变这一点，科威助力模型Bahdanau，在预测词元时，如果不是所有输入词元都相关，模型将仅对齐输入序列中与当前预测相关的部分，这是通过将上下文变量视为注意力集中的输出来实现的

模型图：

上图就是一个带此结构的编码解码器模型
图中，sources经过embedding后进入RNN形成 编码器，编码器对于每次词的输出作为key和 value（它们是同样的）
解码器RNN对上一个词的输出是query
attention的输出与下一个词的词嵌入合并后进入下一次的RNN

自注意力机制

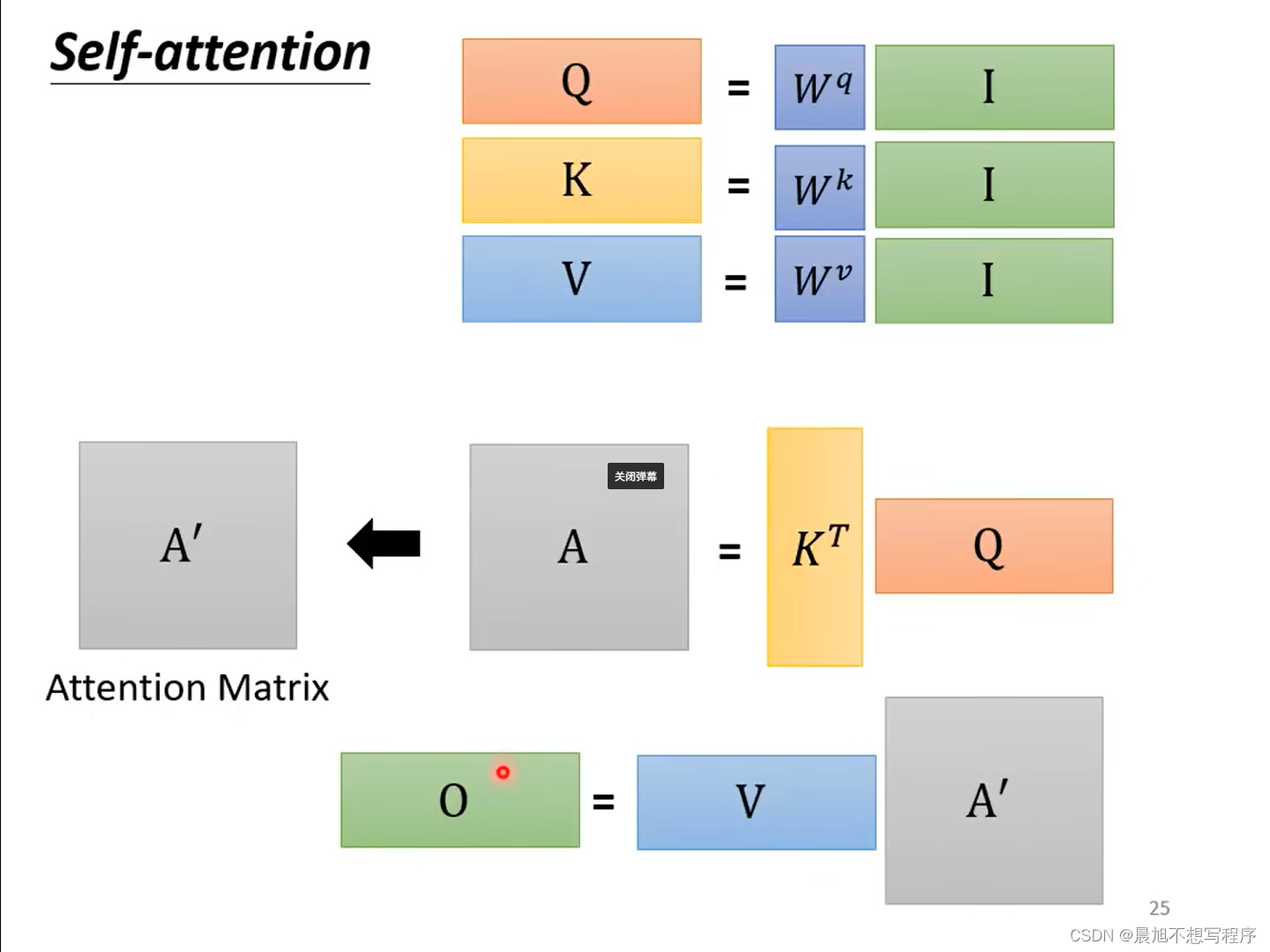
所谓自注意力就是KVQ都是来自同一个输入所得

注：与RNN不同，自注意力机制拥有很高的并行度，复杂度较高

位置编码

自注意力并没有记录位置信息，所以要用到位置编码，位置编码将位置信息注入到输入里

位置编码用于表示绝对或者相对的位置信息，可以是设定好的固定参数，也可以是由学习所得

如下就是一种固定好的正余弦函数表示的固定位置编码

假设长度为n的序列是n×d的shpe的X，那么使用n×d的shape的位置编码矩阵P来输出X+P作为自编码输入

P $ \in $ $ R^ {n\times d} $ : $ p_ {i,2j} $ = $ \sin $ ( $ \frac {i}{10000^ {2j/d}} $ ), $ p_ {i,2j+1} $ = $ \cos $ ( $ \frac {i}{10000^ {2j/d}} $ )

如图（比较抽象，花了很久理解）
首先横坐标是不同位置索引的数据，不同的函数图像是设定好的，比如可以设定256个col，这个超参数的大小就蕴含了输出向量可以获取的位置信息，这样就保证了不同位置的输出绝对不一样，例如row为0时的输出为[1,0,1,0,1,0,1,0...]，不可能存在第二个col输出与此相同的情况，而col的个数代表了蕴含的信息量,越多可获取就越多

位置编码与二进制编码类似的效果

二进制表示例：使用三位二进制数表示八个数字的信息

如图所示，每一个位置，也就是横着拿出来一条，绝对找不到与之相等的一条了，这是不可能的

transformer

transformer架构

transformer的编码器是由多个相同的层叠加而成的，每个层都有两个子层

第一个子层是多头自注意力汇聚，第二个子层是基于位置的前馈网络

收到残差网络的启发，每个子层都采用了残差连接

transformer解码器也是由多个相同的层叠加而成的，并且层中使用了残差连接和层规范化。除了编码器中描述的两个子层之外，解码器还在这两个子层中插入了第三个子层，成为编码器-解码器注意力层，

多头注意力

多头注意力是一种特殊的使用自注意力的结构

是说同一k,v,q，希望抽取不同的信息，例如短距离关系和长距离关系

多头注意力使用h个独立的注意力池化，合并各个头输出得到最后的输出

有掩码的多头注意力

训练解码器对于序列中一个元素输出时，不应该考虑该元素之后的元素，可以通过掩码来实现，也就是计算$X_i$输出时，假装当前序列长度为$i$

基于位置的前馈网络

也就是图中的逐位前馈网络

实际上就是全连接，batch_size,n—》序列长度,dimension

由于n的长度不是固定的

• 将输入形状由(b,n,d)变换成(bn,d)
• 作用两个全连接层
• 输出形状由(bn,d)变换回(b,n,d)
• 等价于两层核窗口为1的一维卷积层

层归一化

self attention

加性注意力

一般来说，当查询和键是不同长度的向量时，可以使用加性注意力作为评分函数

k $ \in $ $ R^ {h\times k} $ , $ W_ {q} $ $ \in $ $ R^ {h\times q} $ ,v $ \in $ $ R^ {h} $
a(k,q)= $ v^ {T} $ $ \tanh $ ( $ W_ {k} $ k+ $ W_ {q} $ q)

等价于将key与value合并起来后放入到一个隐藏大小为$h$，输出大小为1的单隐藏层MLP

缩放点积注意力

直接使用点积可以得到计算效率很高的评分函数，但是点积操作需要K与Q拥有相同的长度d，此时如果将

a(q, $ k_ {i} $ )= $ \langle $ q, $ k_ {i} $ $\rangle$ /$\sqrt {d} $

除一个根号d的目的是为了消除长度的影响

现在使用的都是点乘attention