画图题
例题7
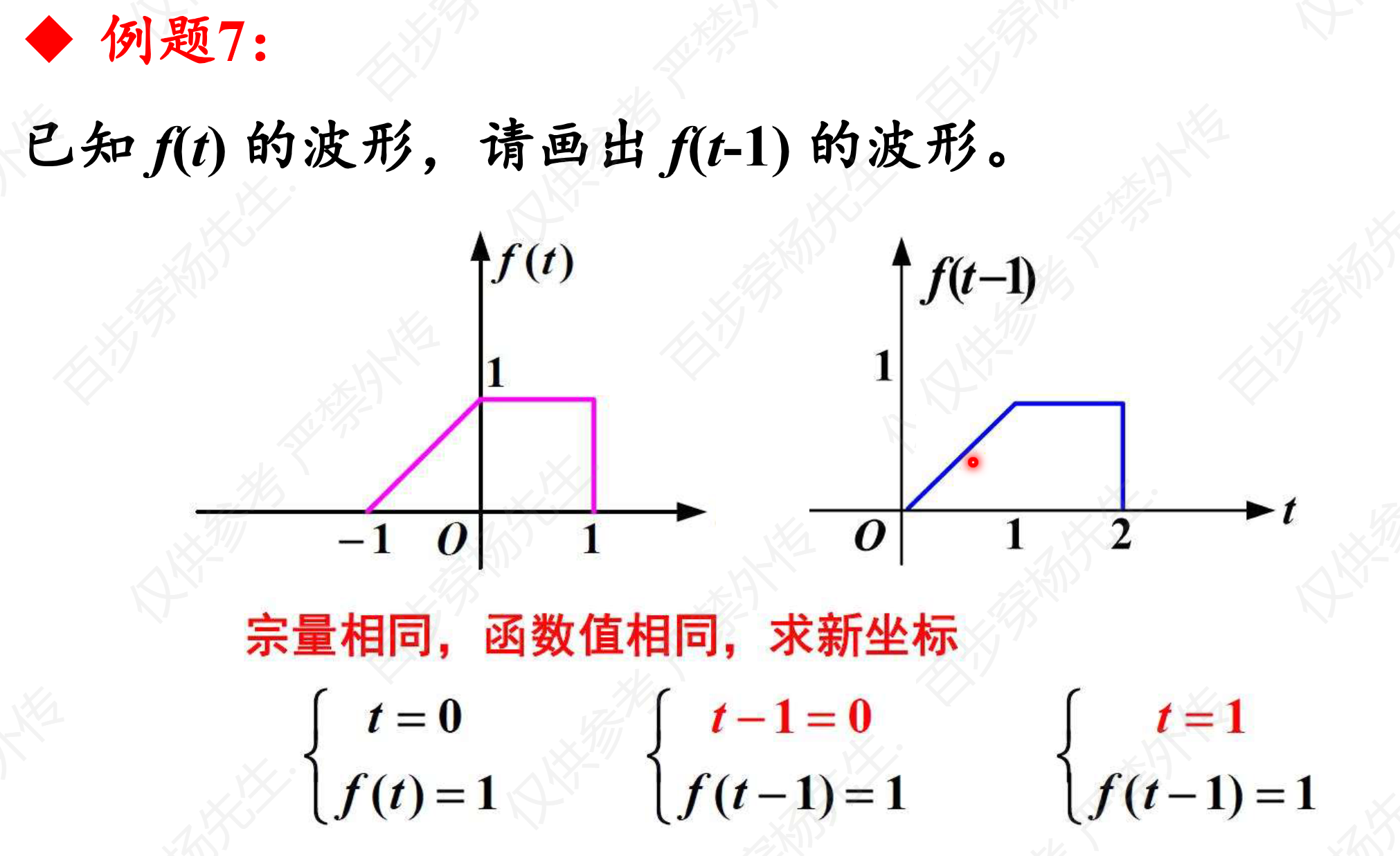
例题8
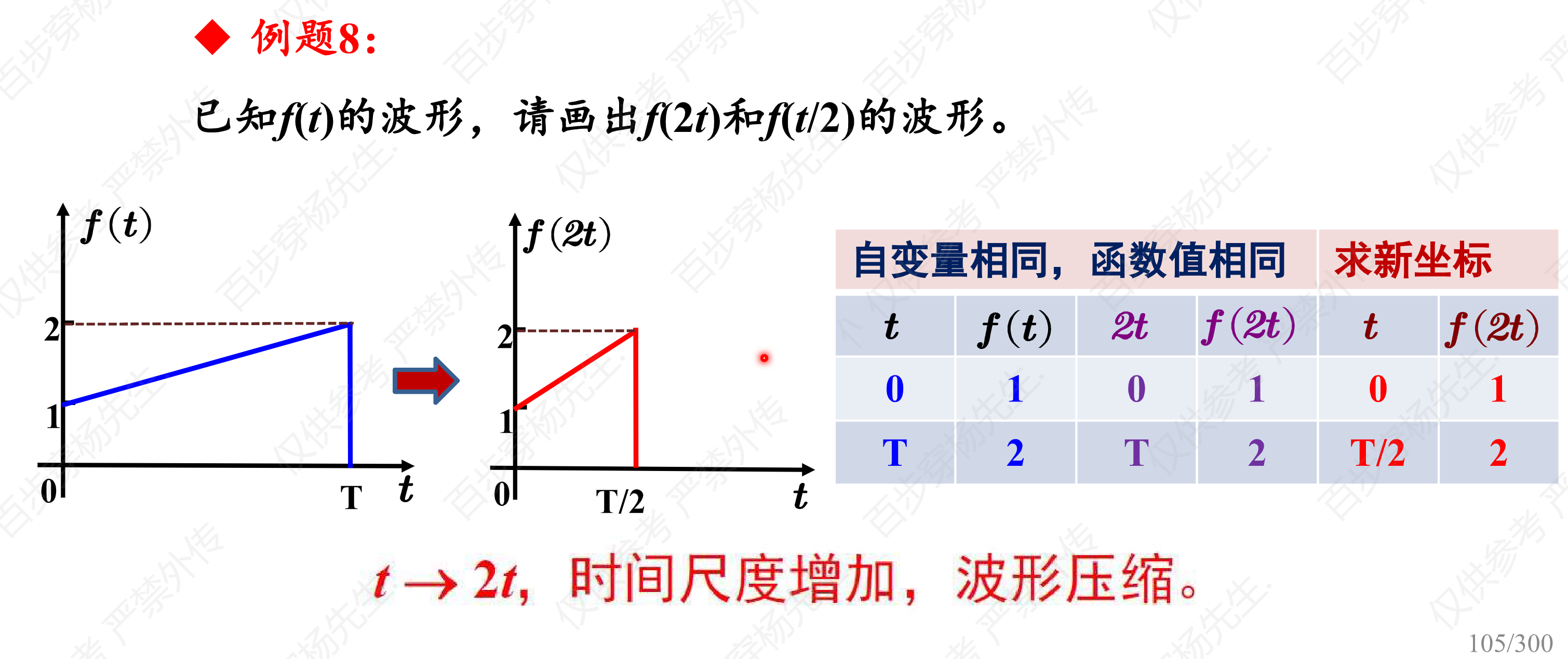
例题9
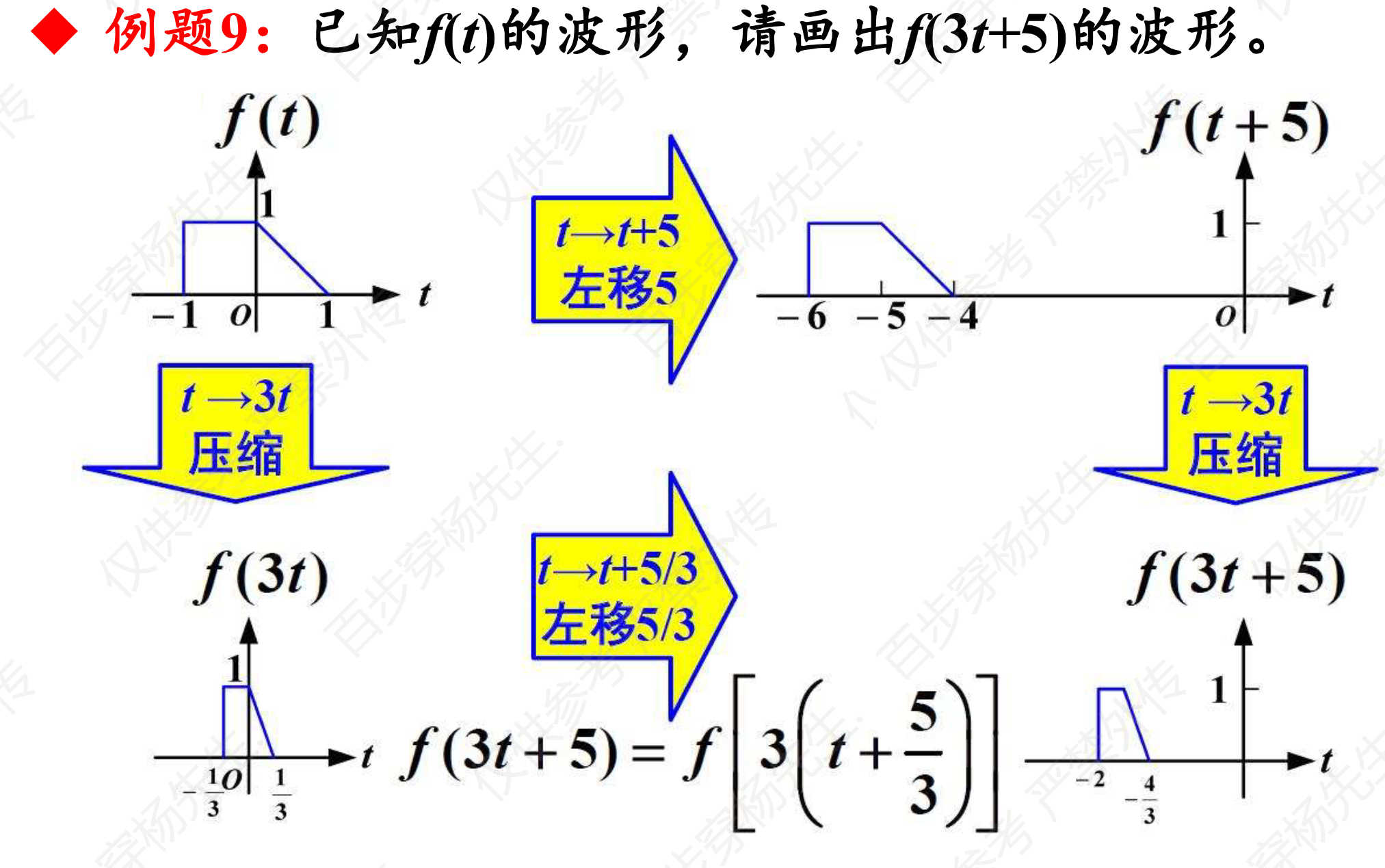
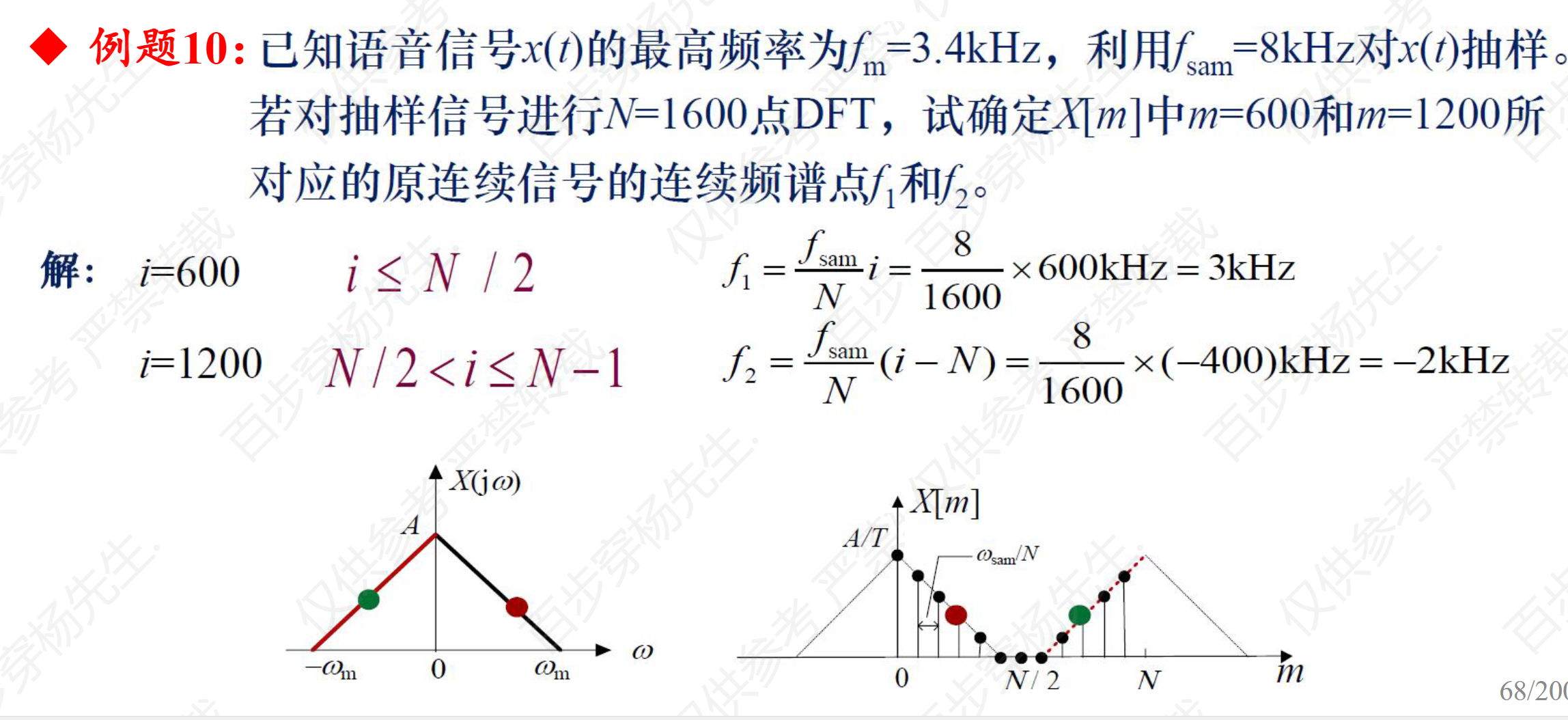
例题10
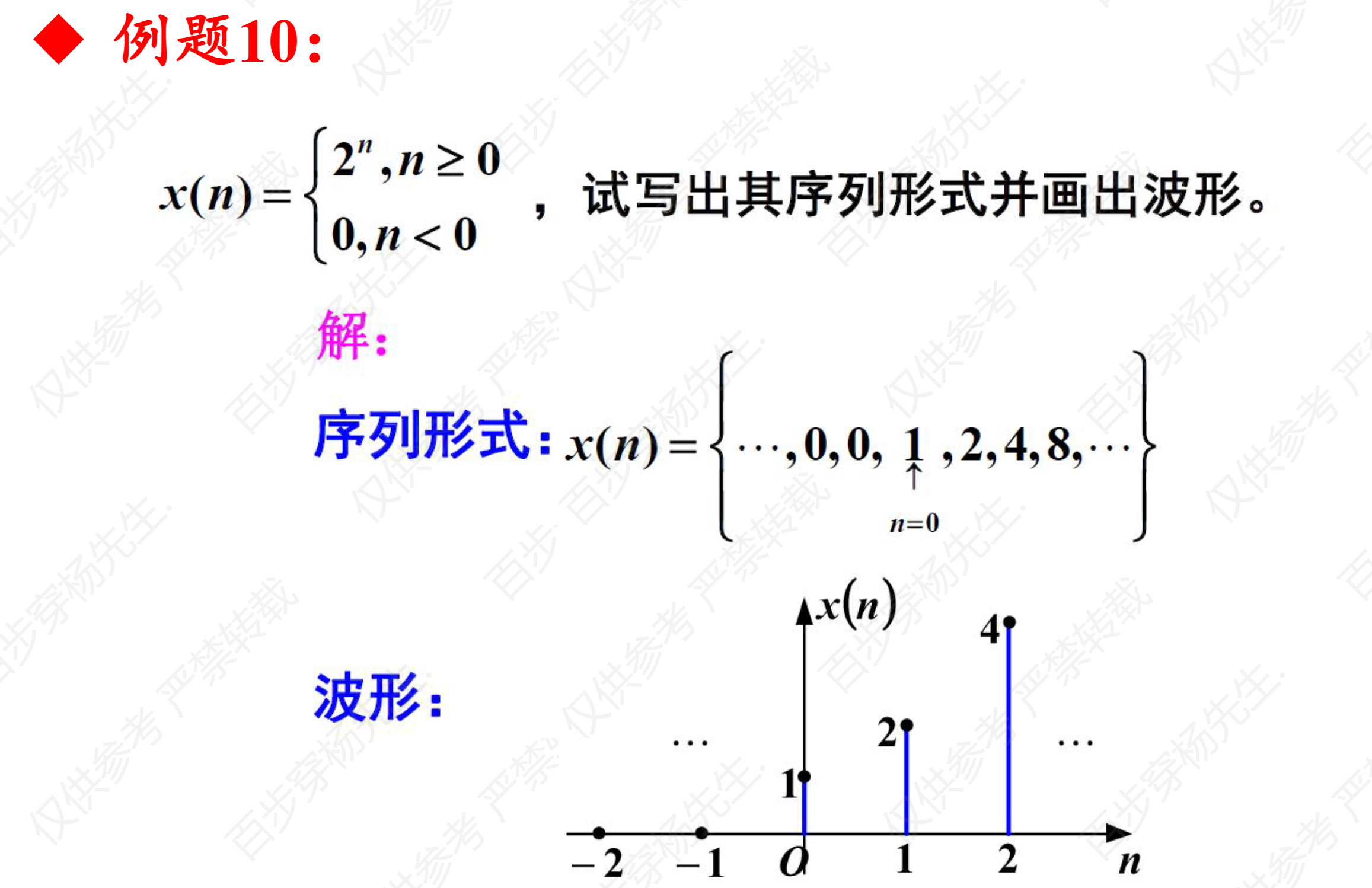
例题11
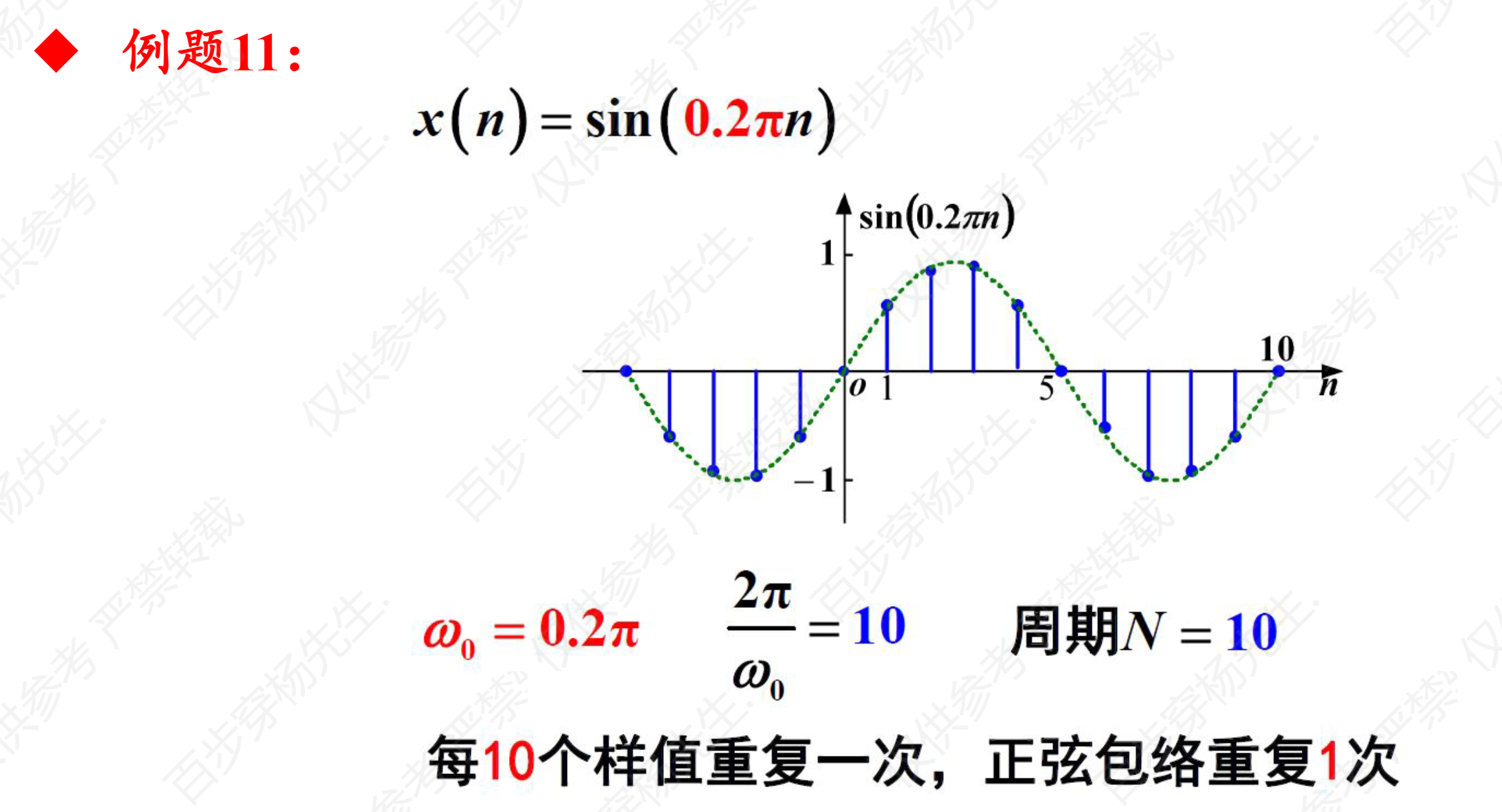
例题12
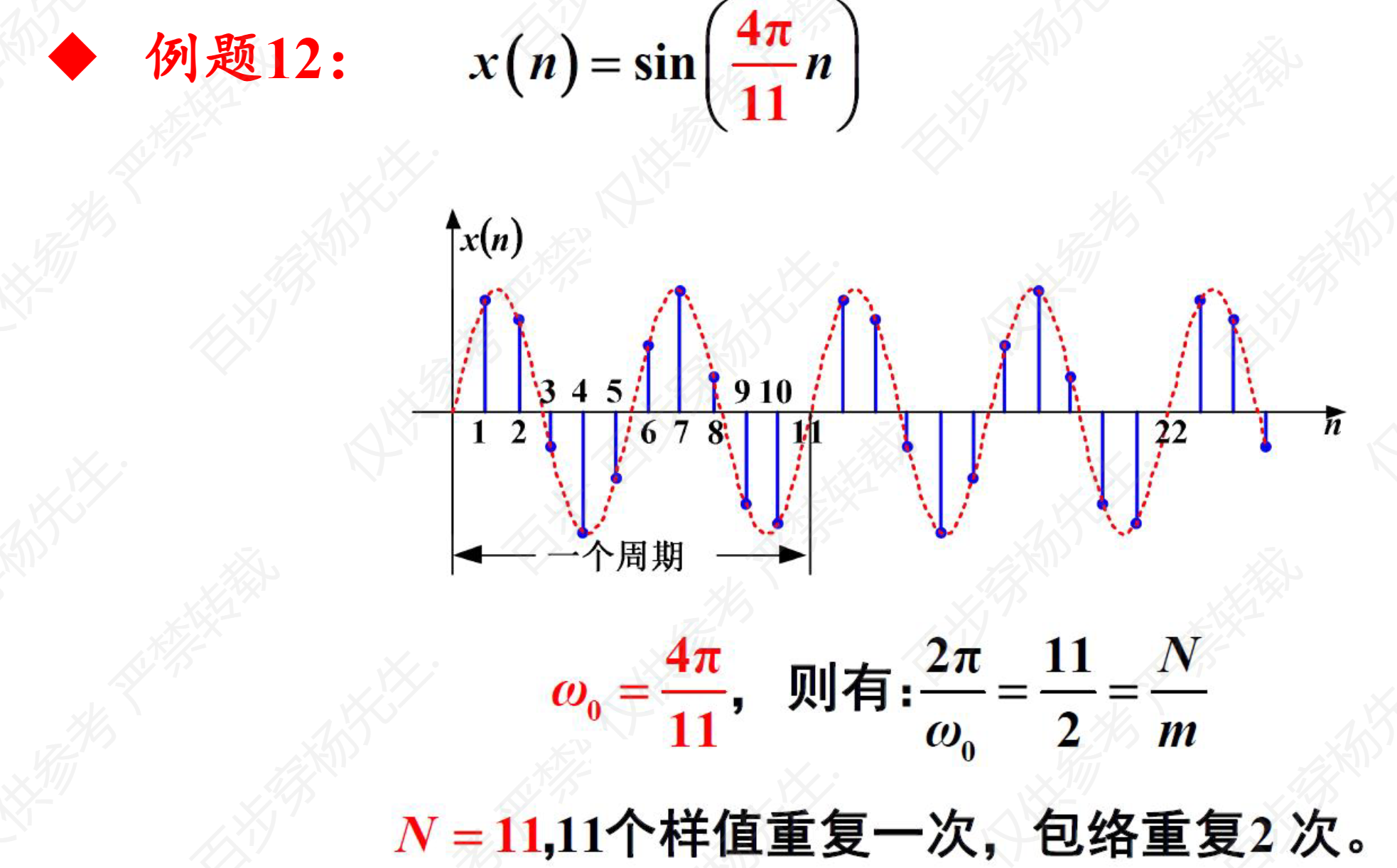
例题18
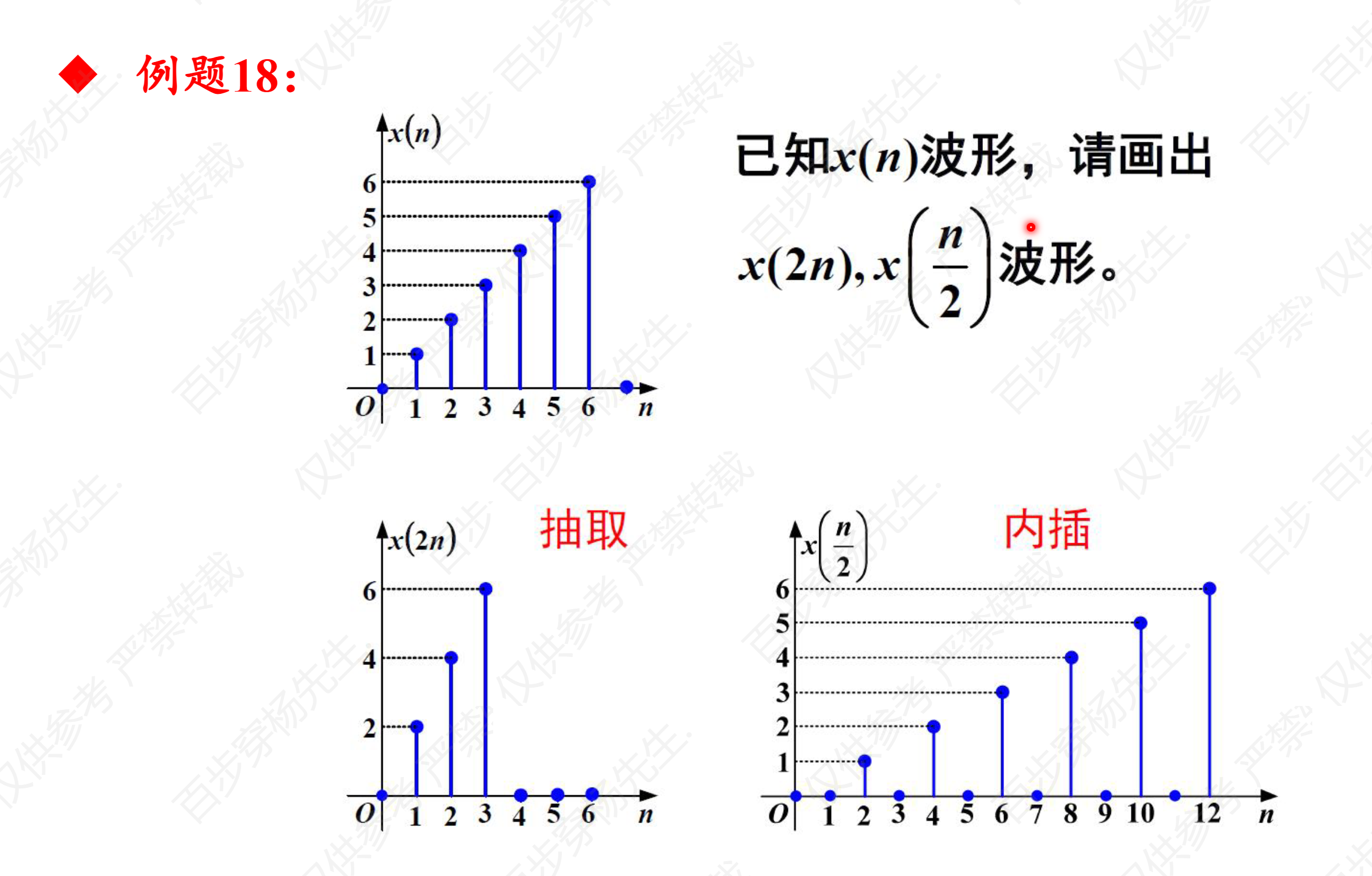
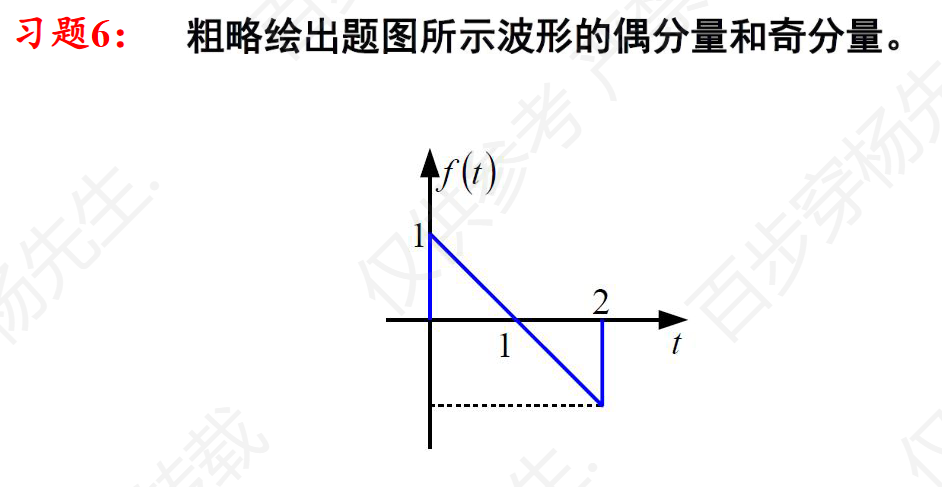
一二章计算题、
例题17

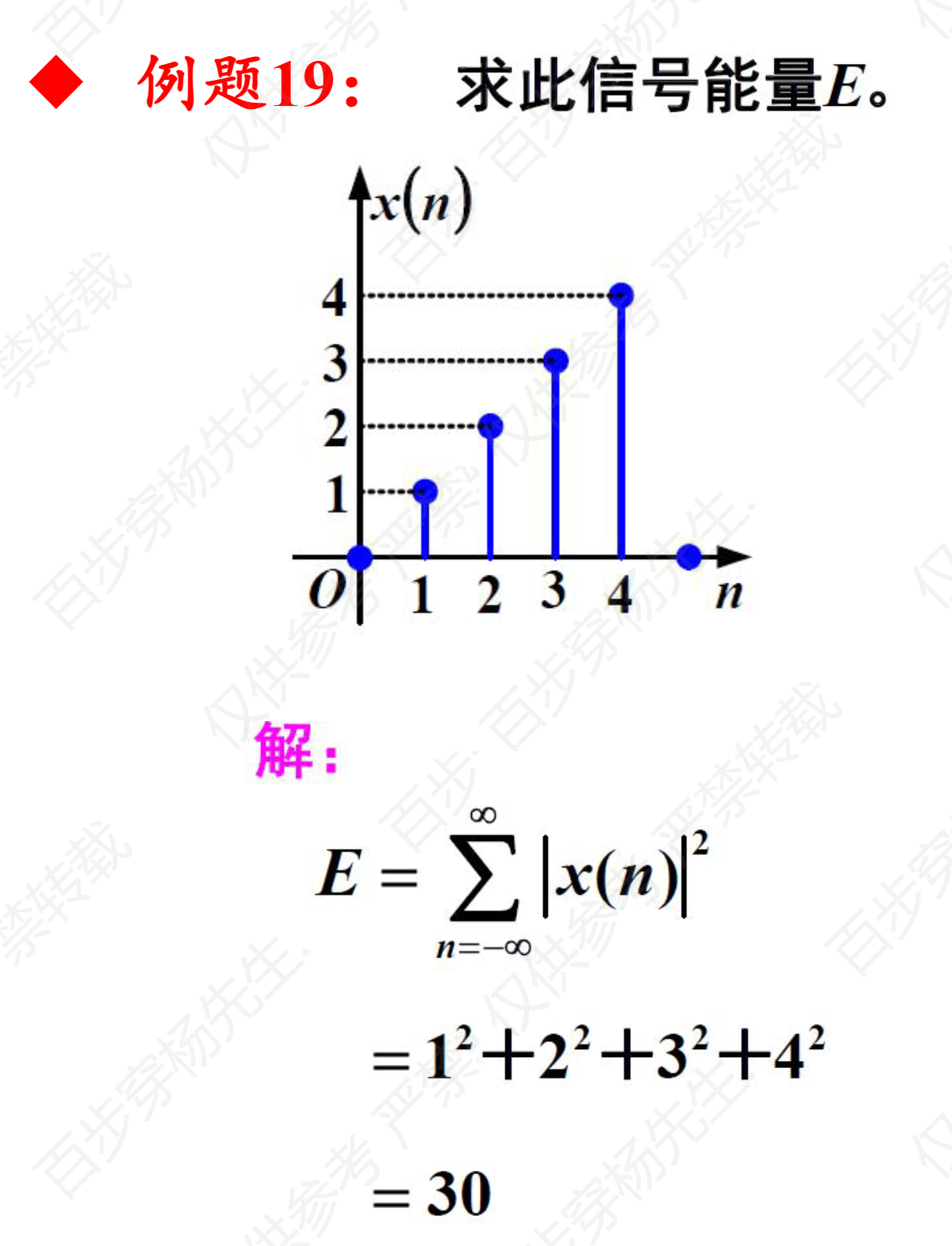
例题19
例题20

例题21

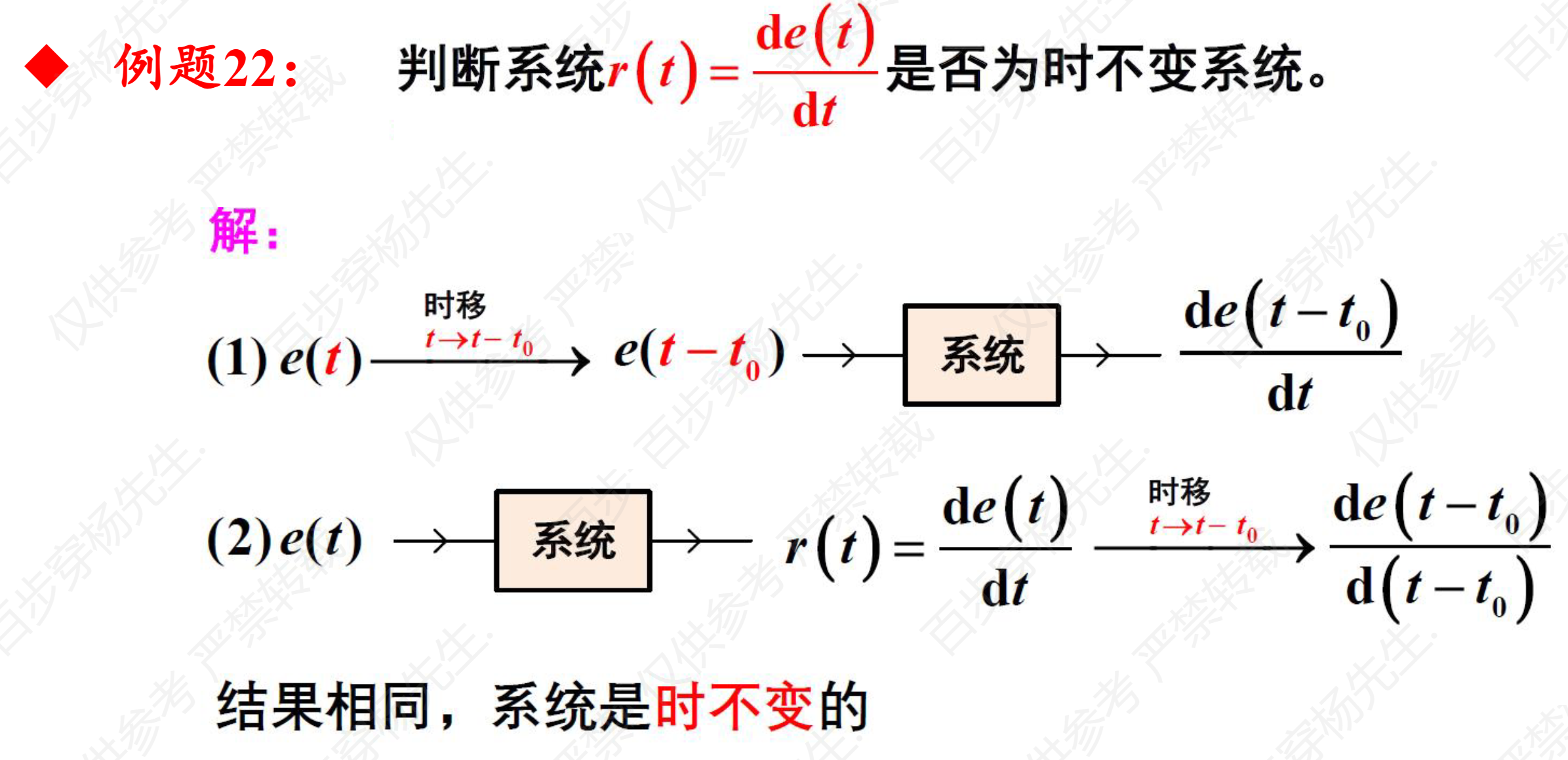
例题22
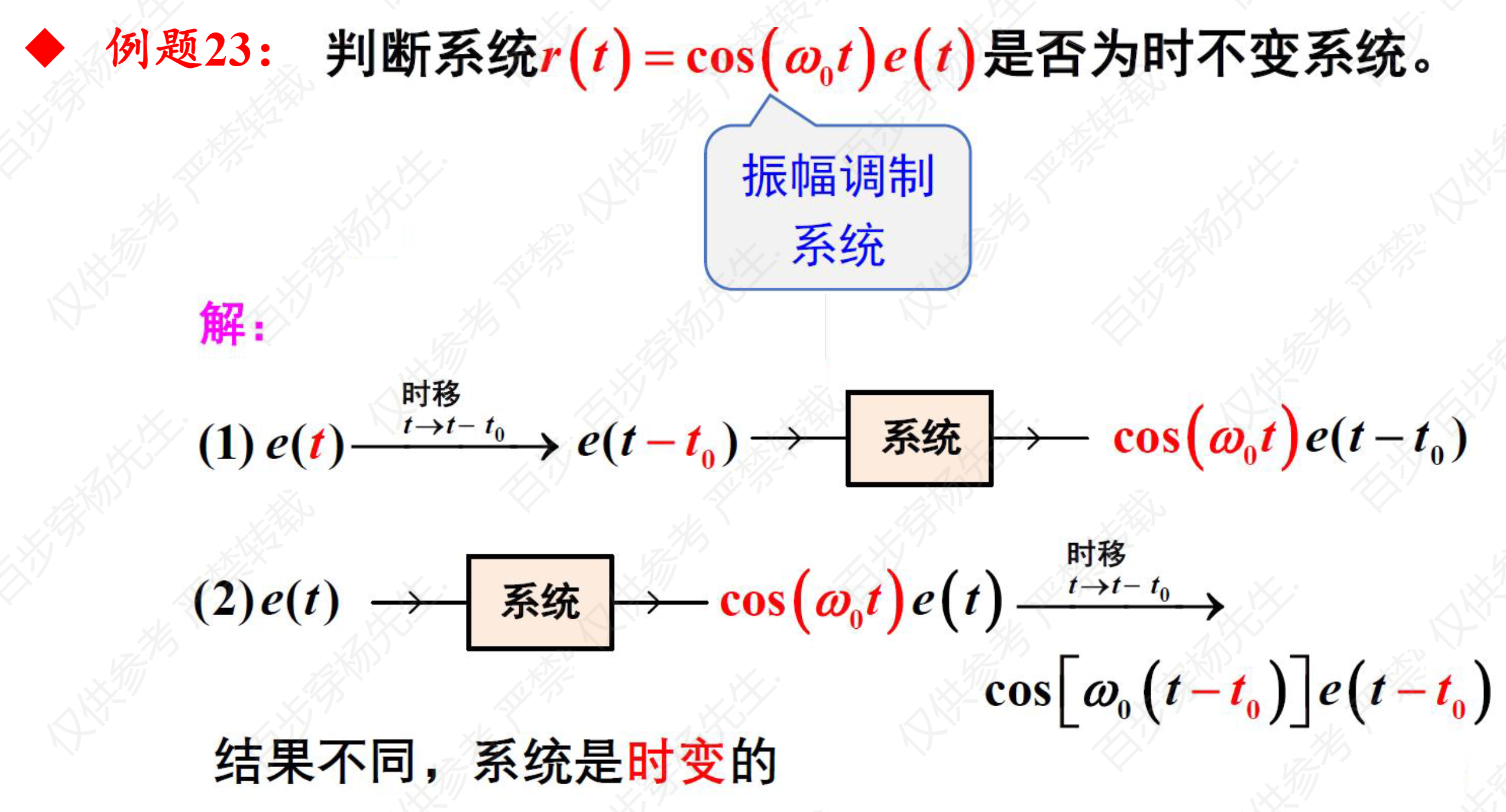
例题23
例题24

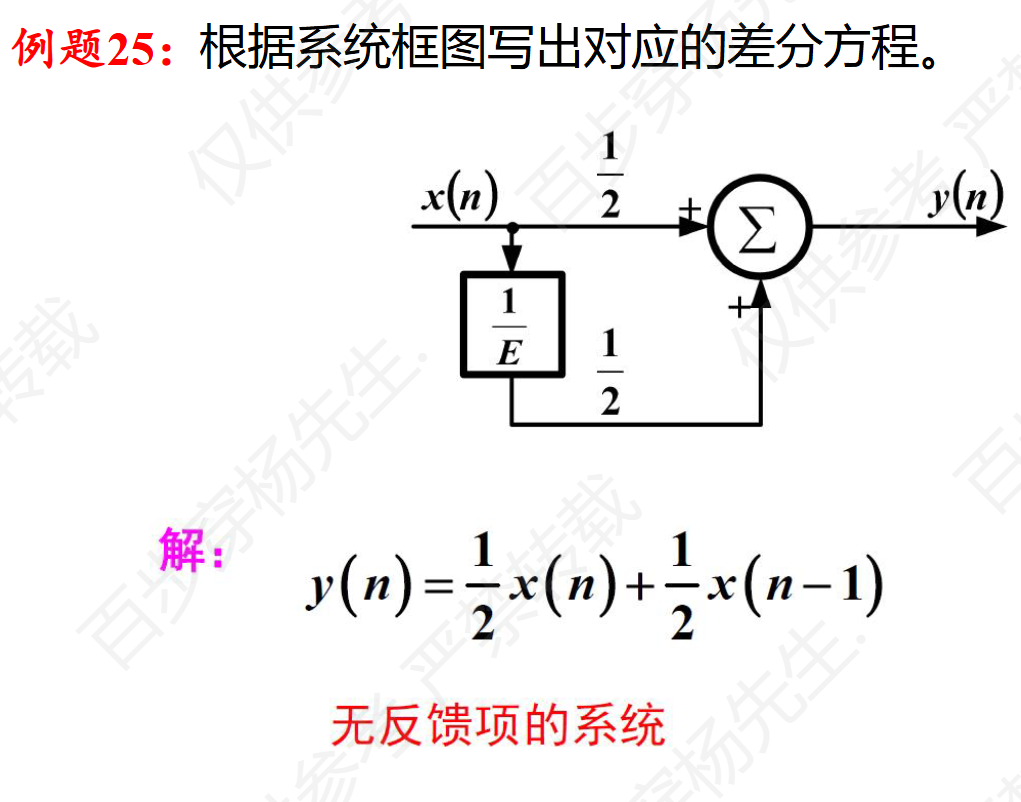
例题25
例题26
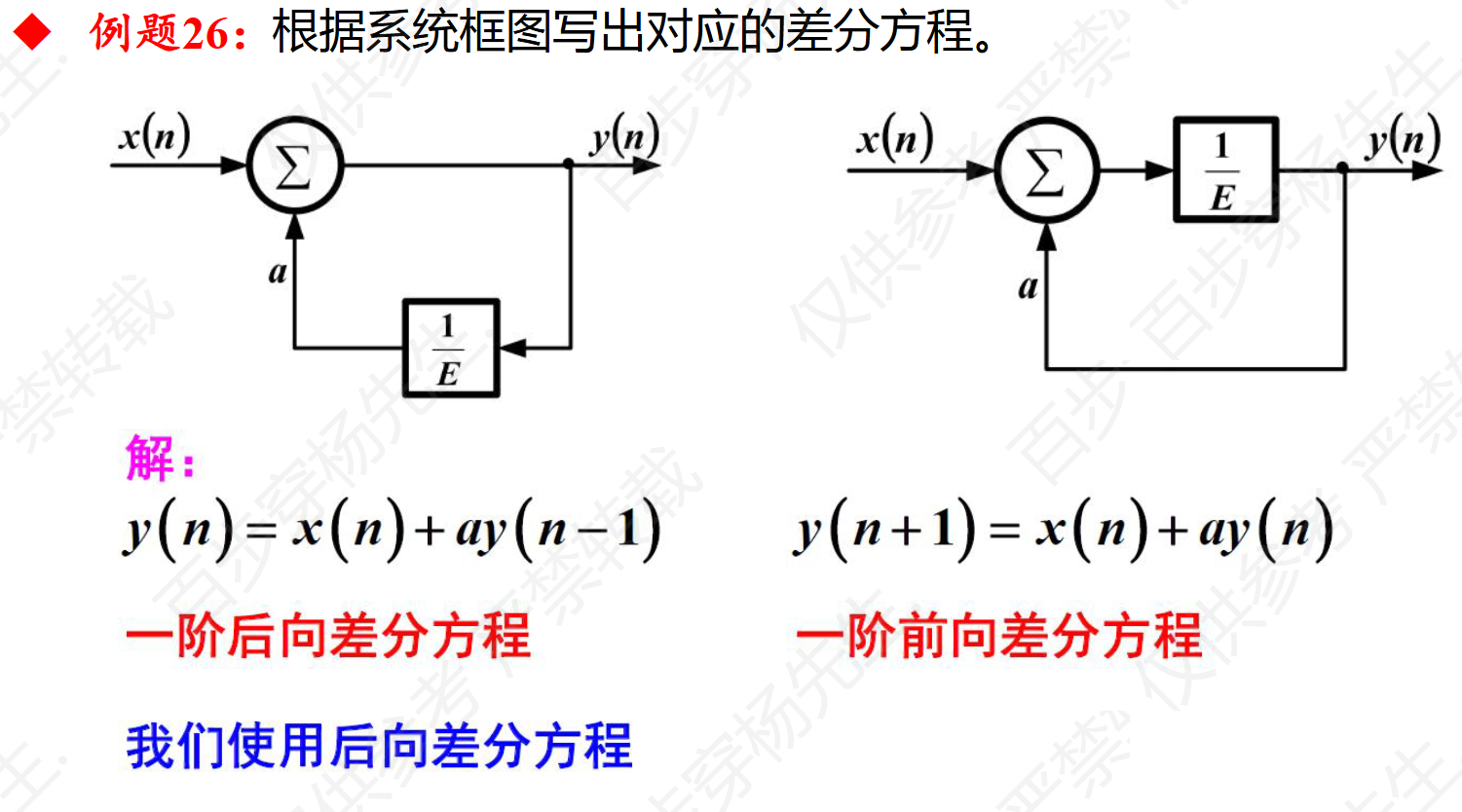
差分方程
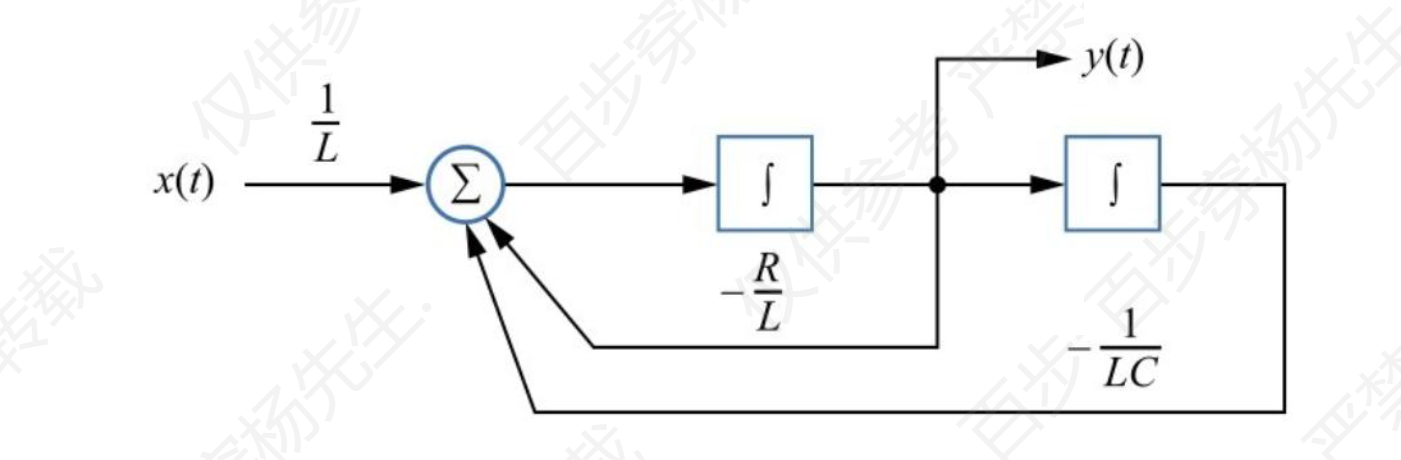
笔记里有写 很麻烦的题
例题25
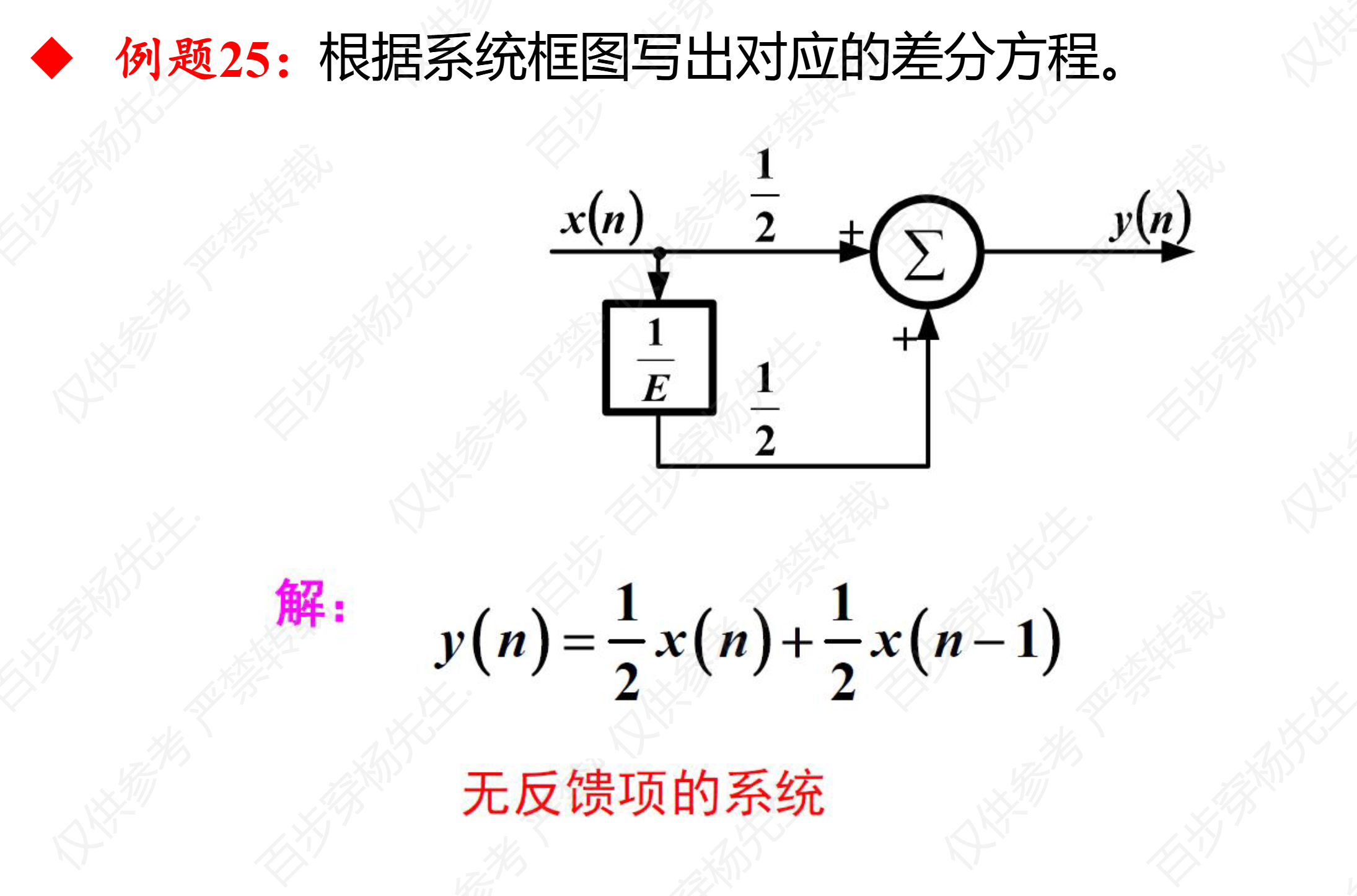
例题26
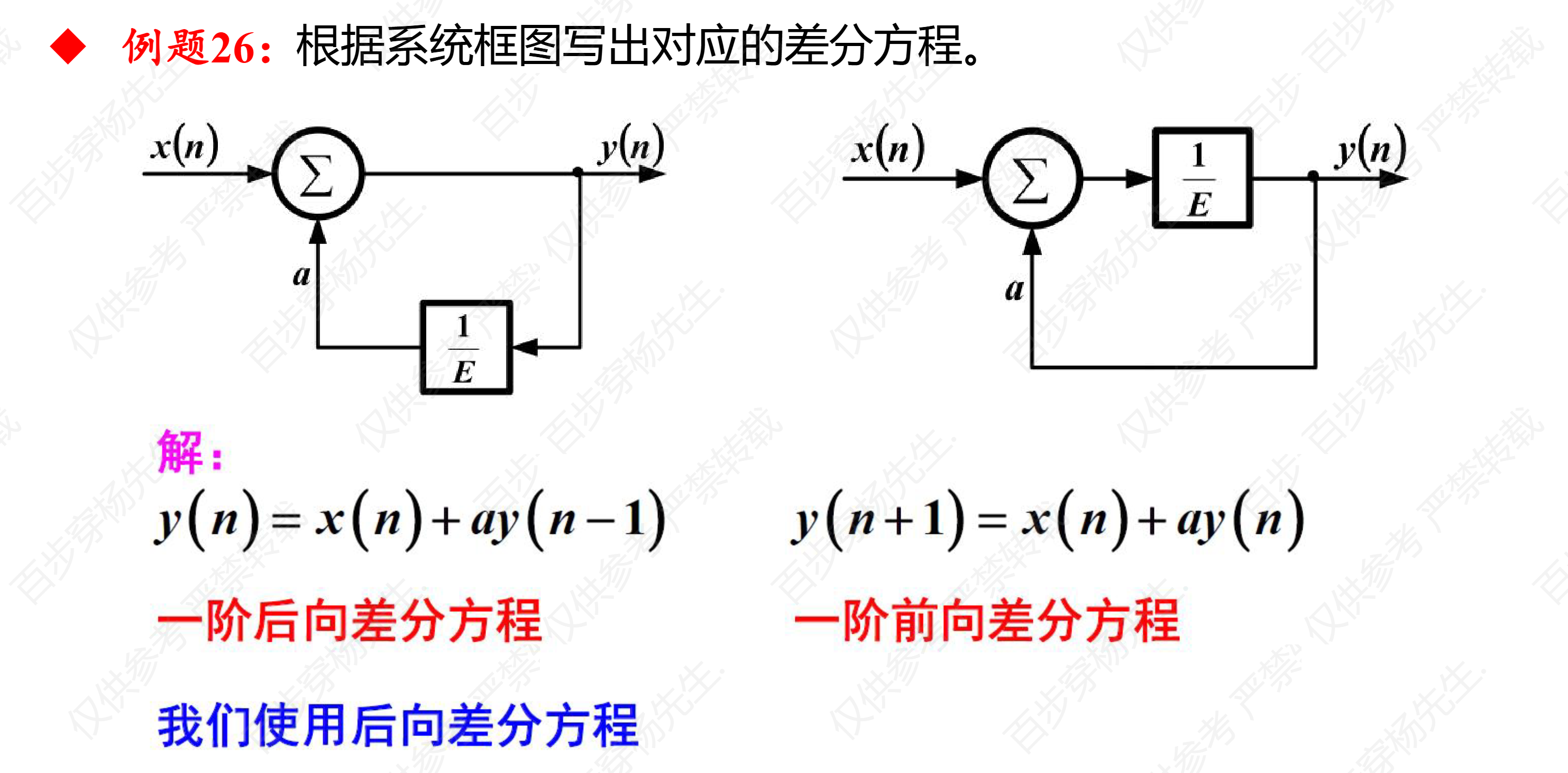
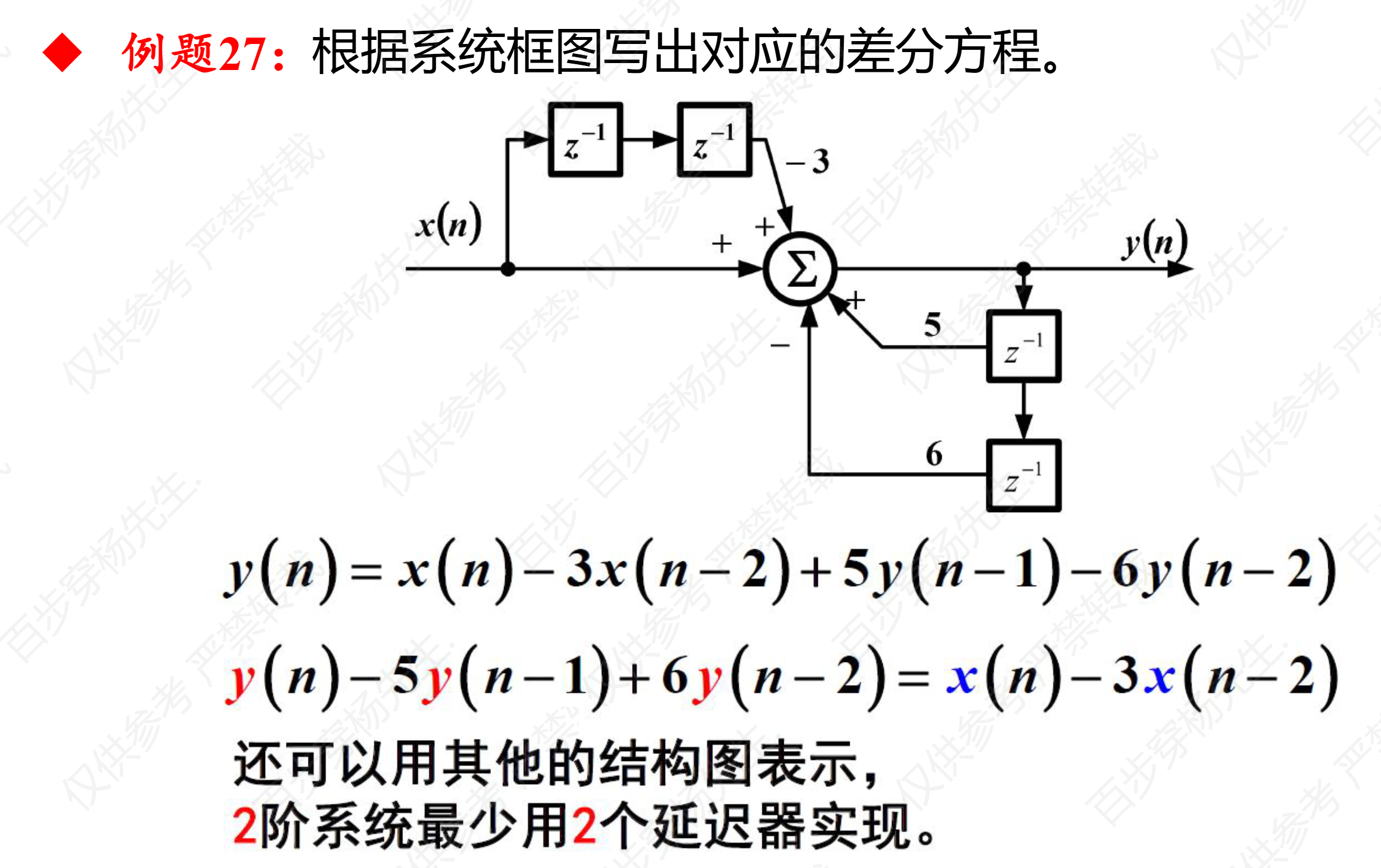
例题27
例题7

卷积计算例题10

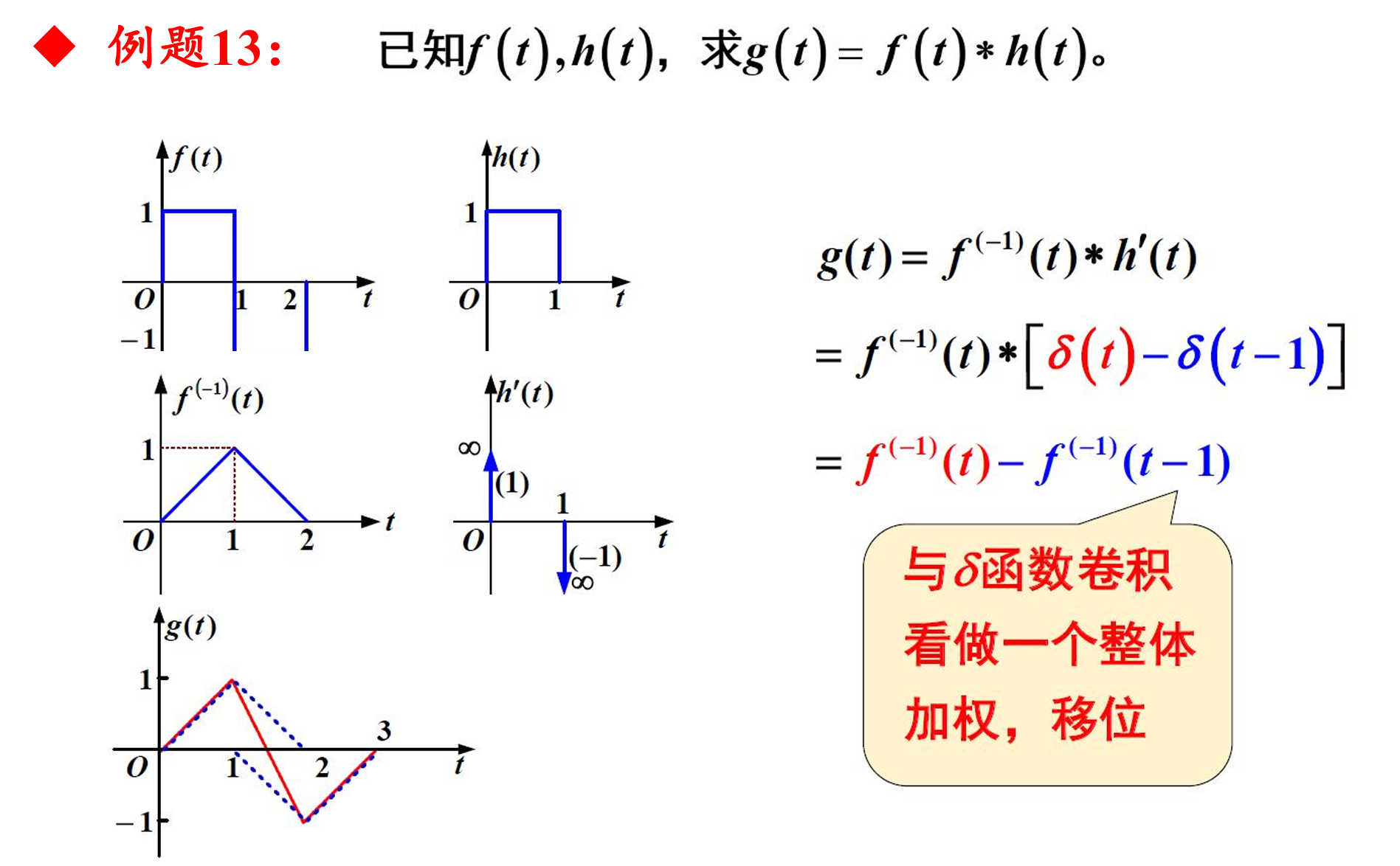
例题13
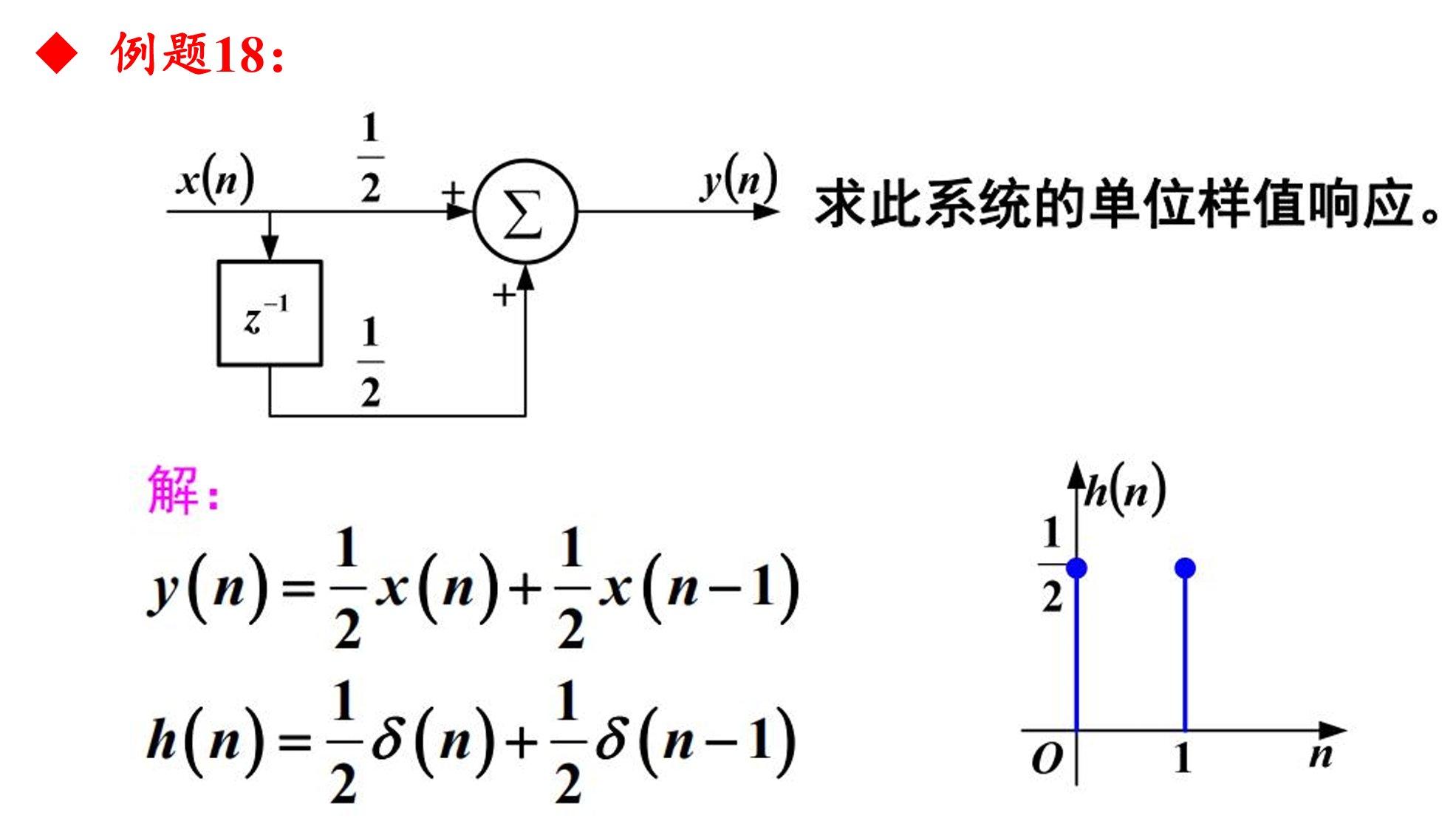
例题18单位样值响应
例题19

例题22

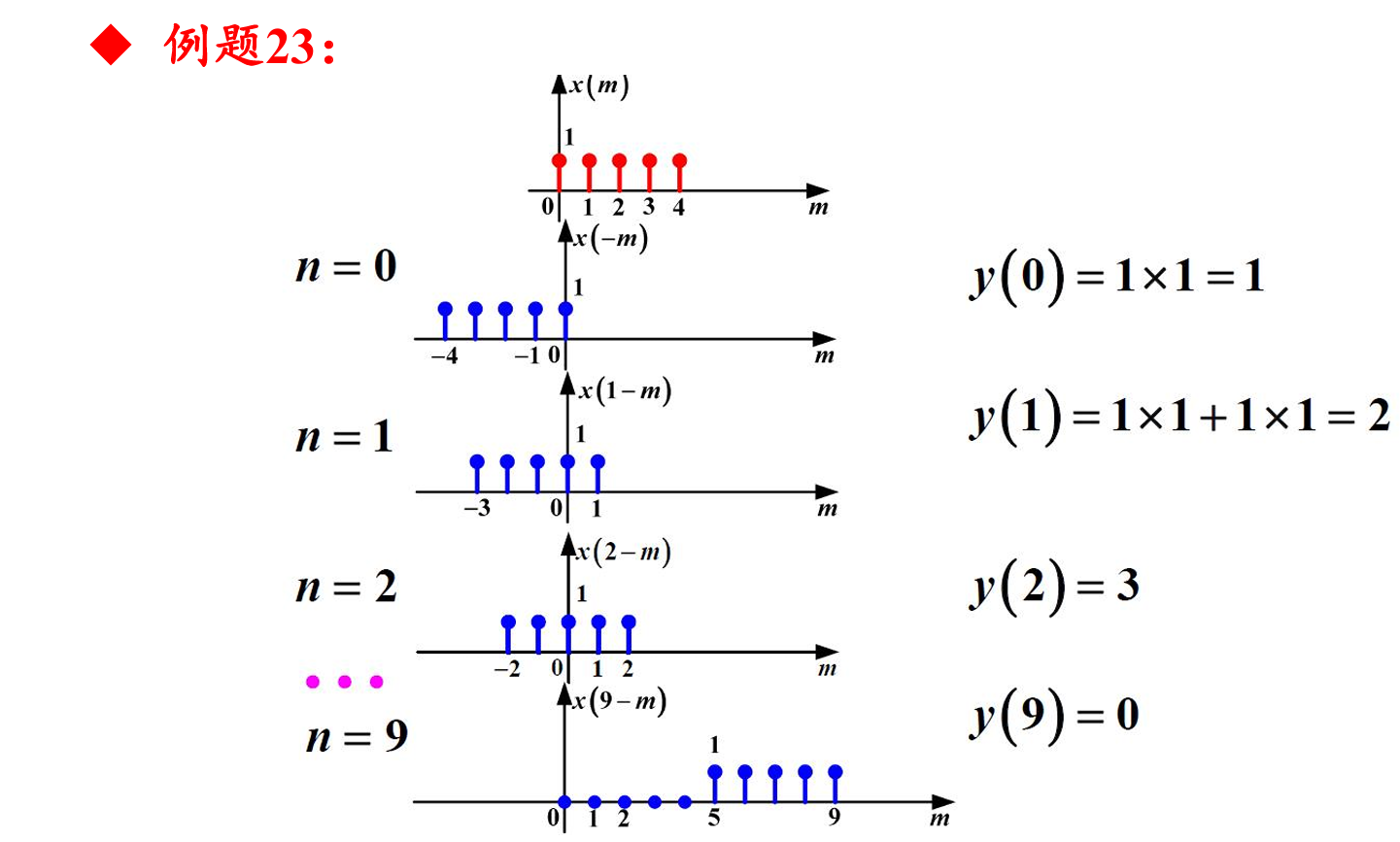
例题23

例题24
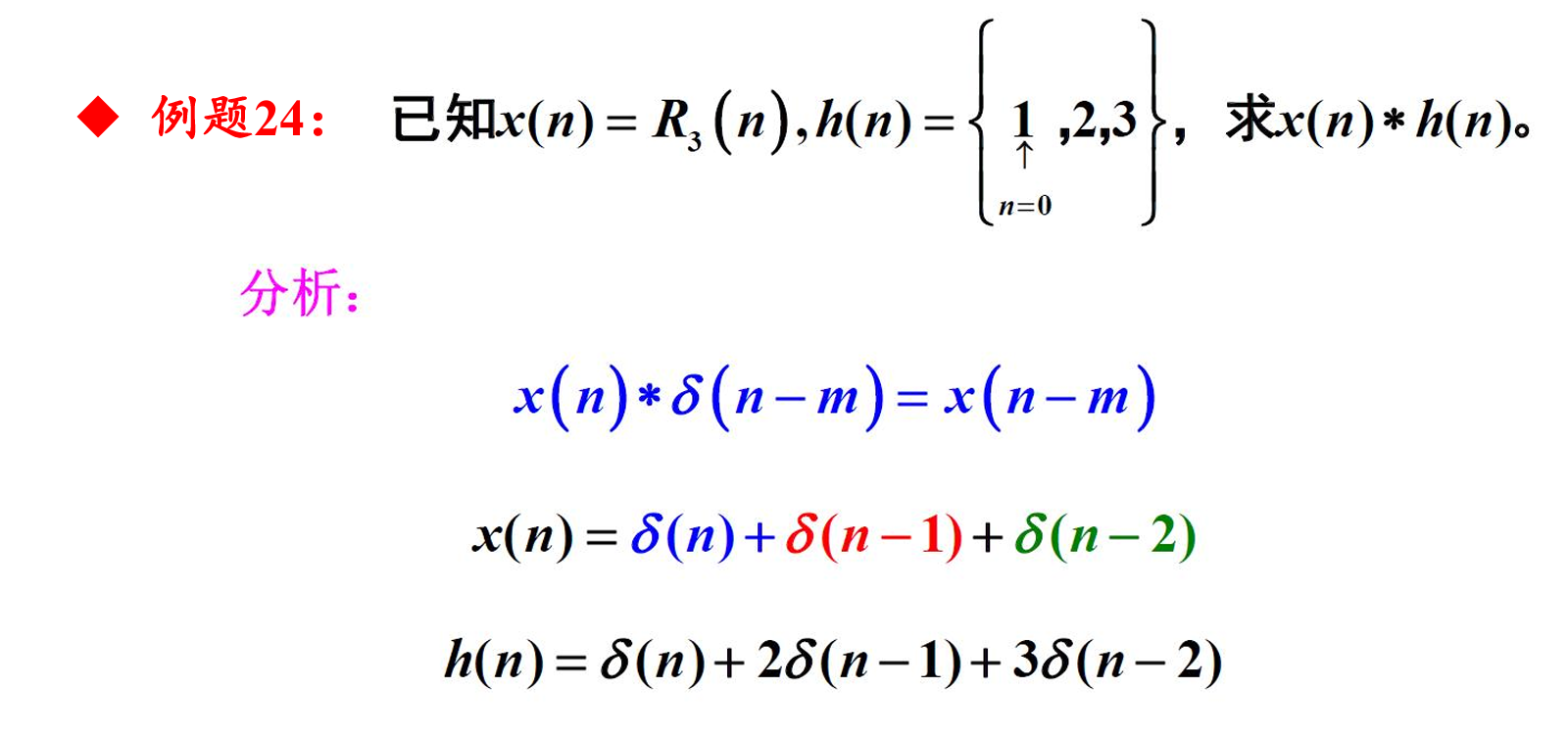
例题25

例题26 **

第三章计算题
例题1

例题5

例题6
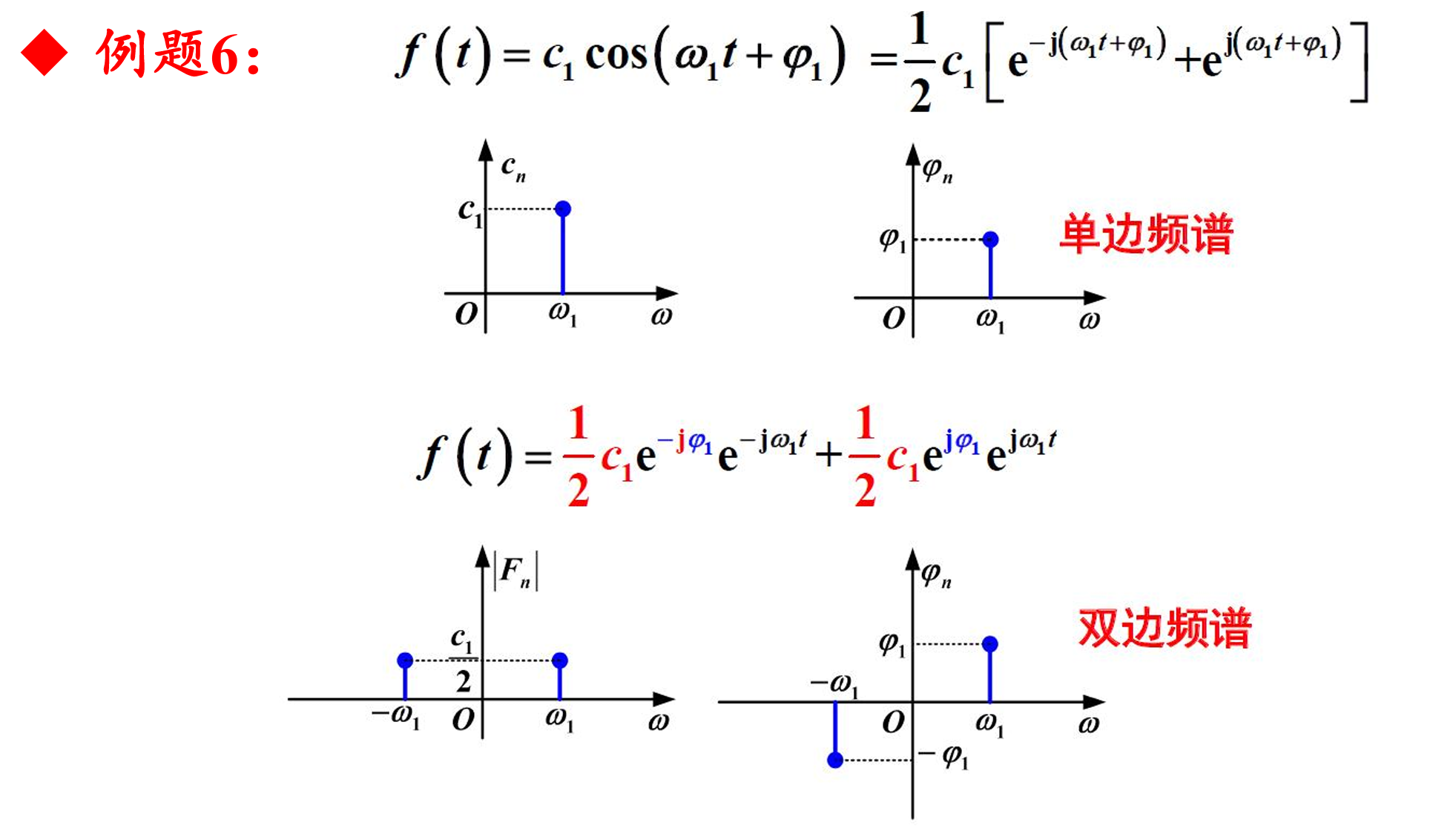
例题7

例题

例题8
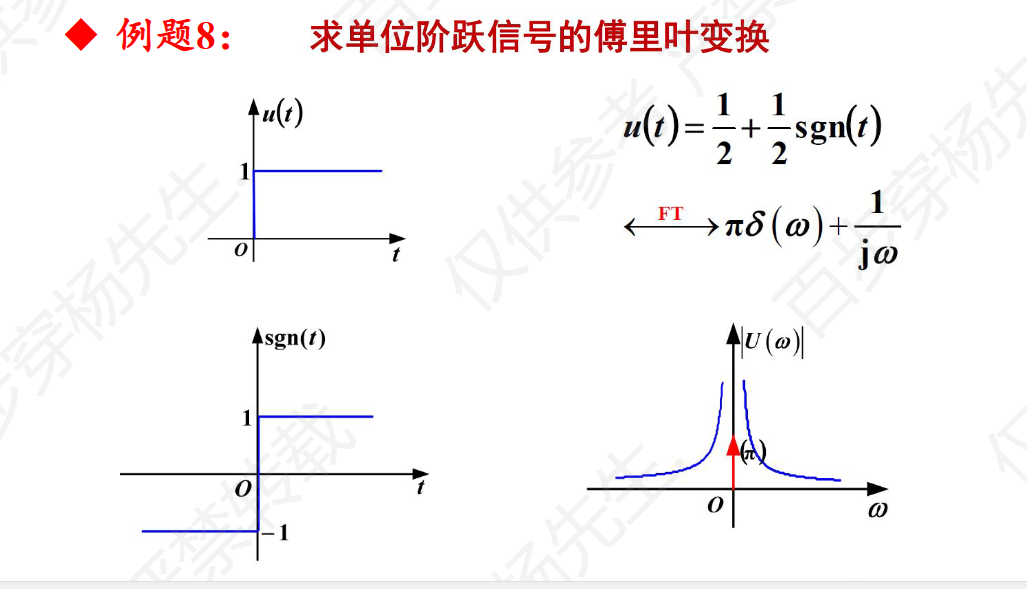
例题9

例题10
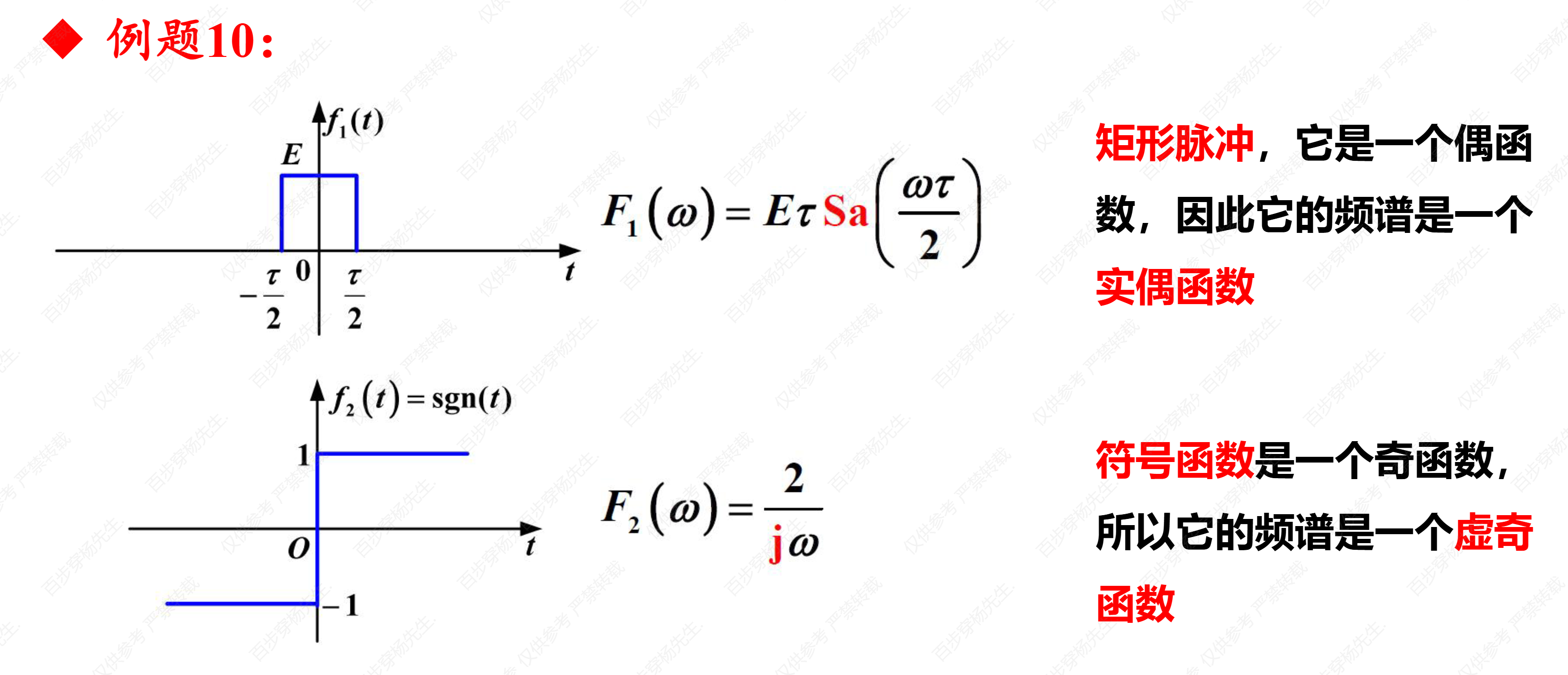
例题11
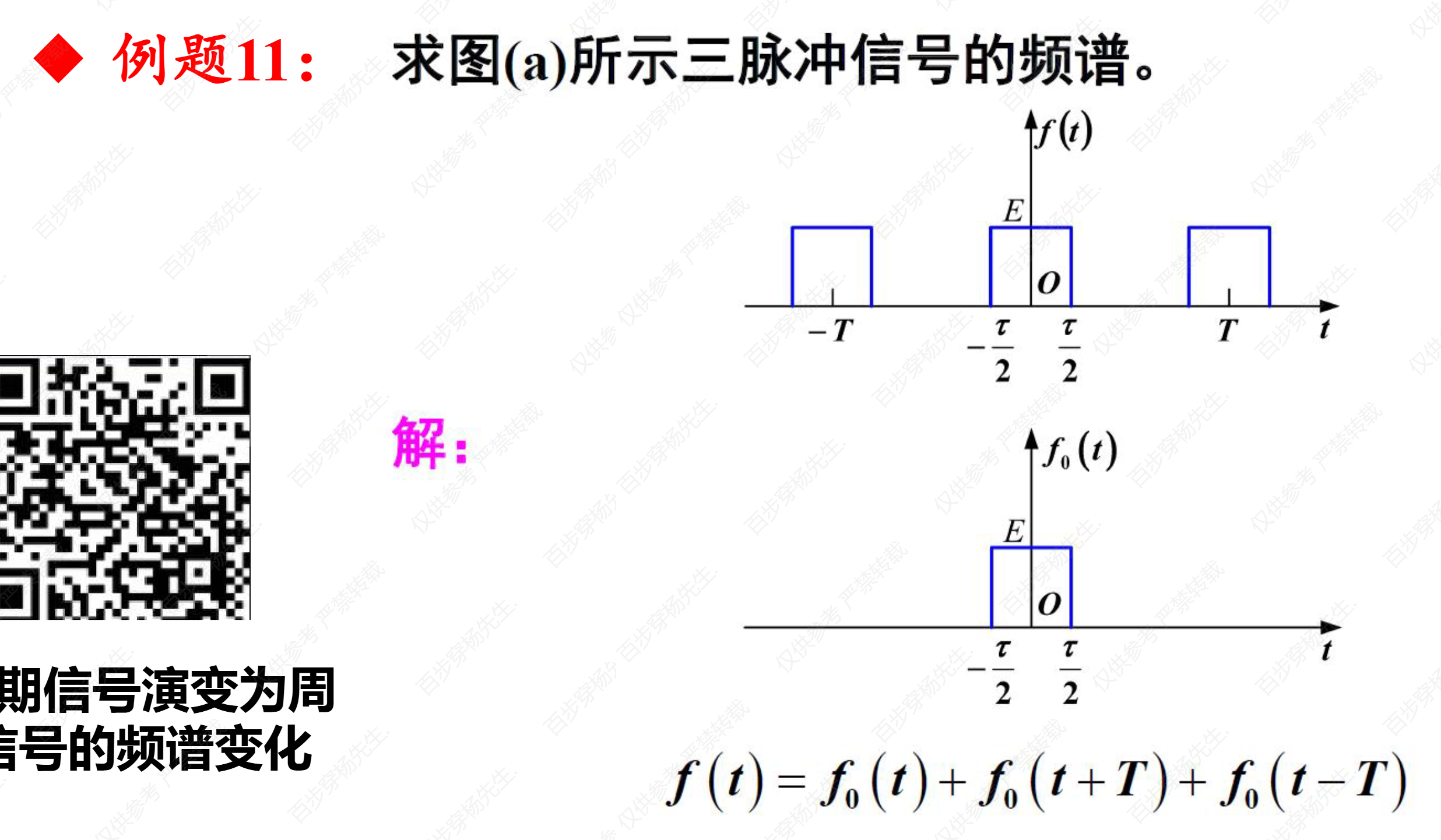
例题12

例题13
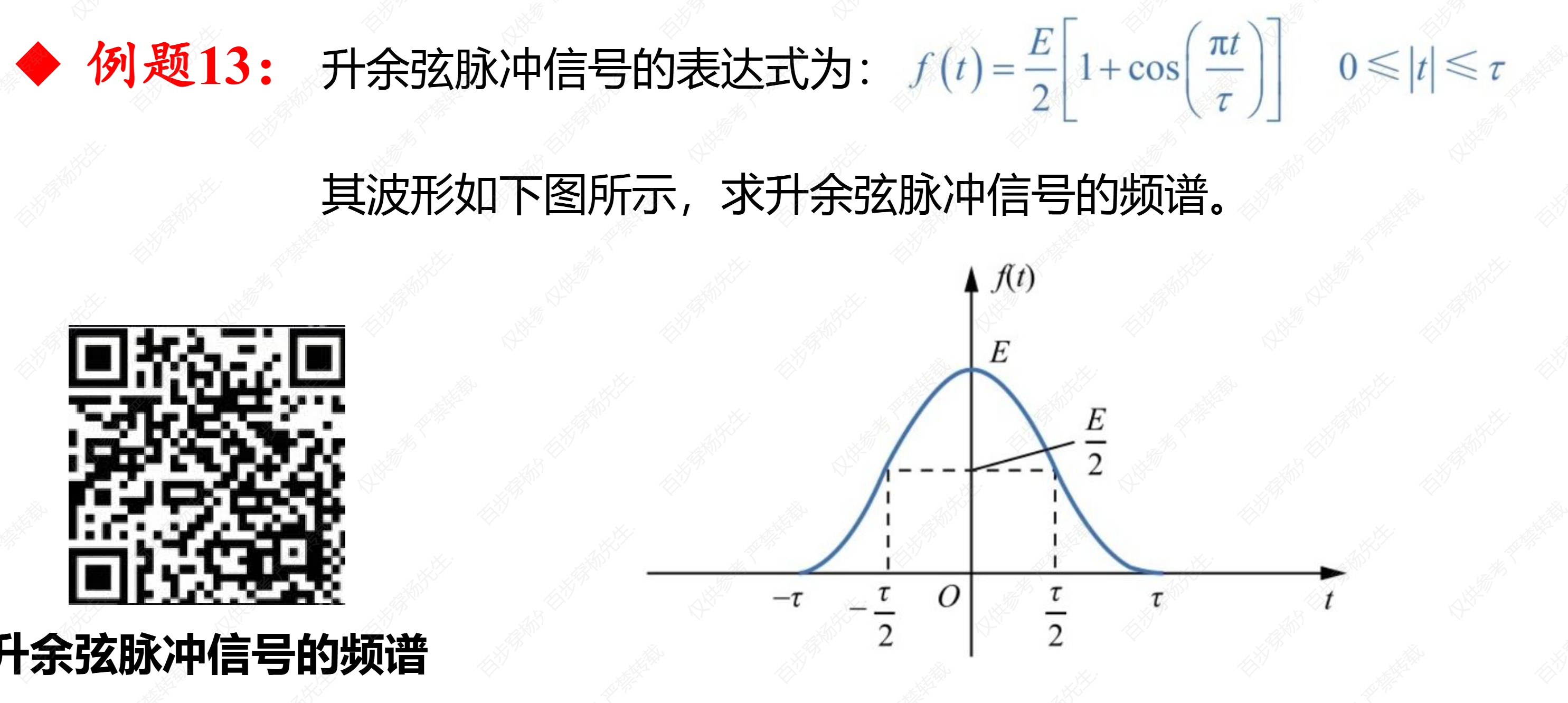
例题14*这里注意复习一下卷积
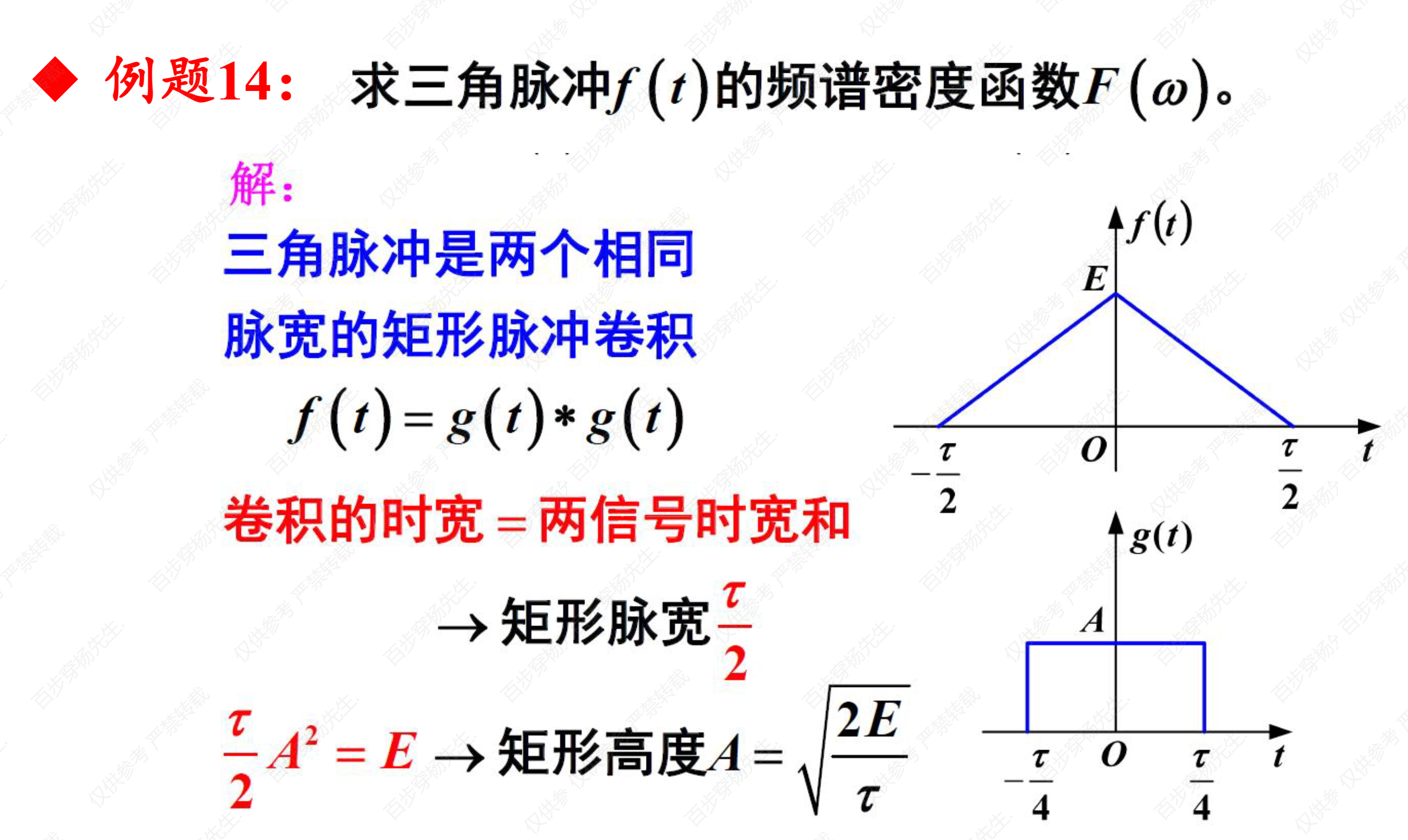
例题15

第四章计算题
例题
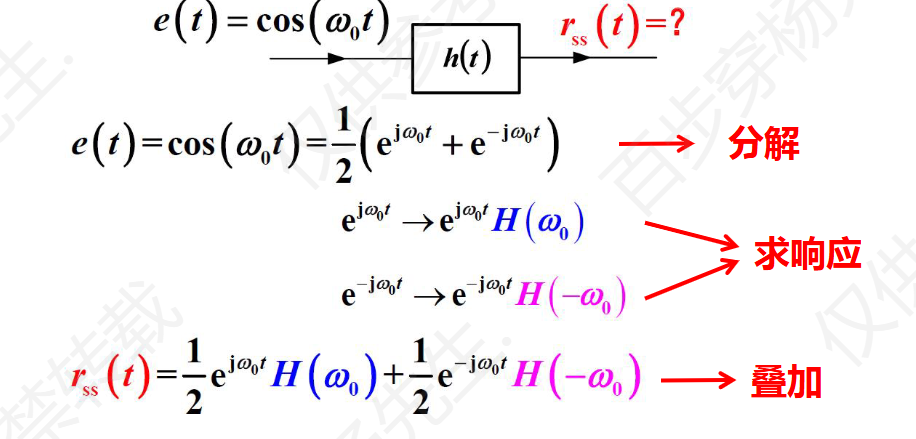
例题1 没看懂

例题2

例题5 无法理解
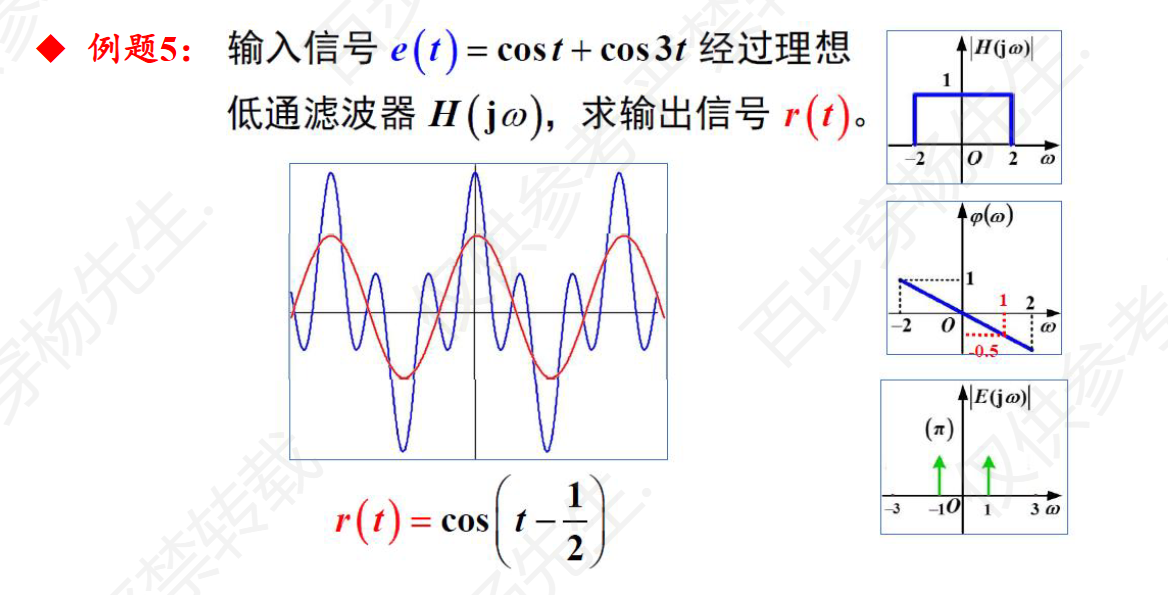
例题7

例题8 *

例题9
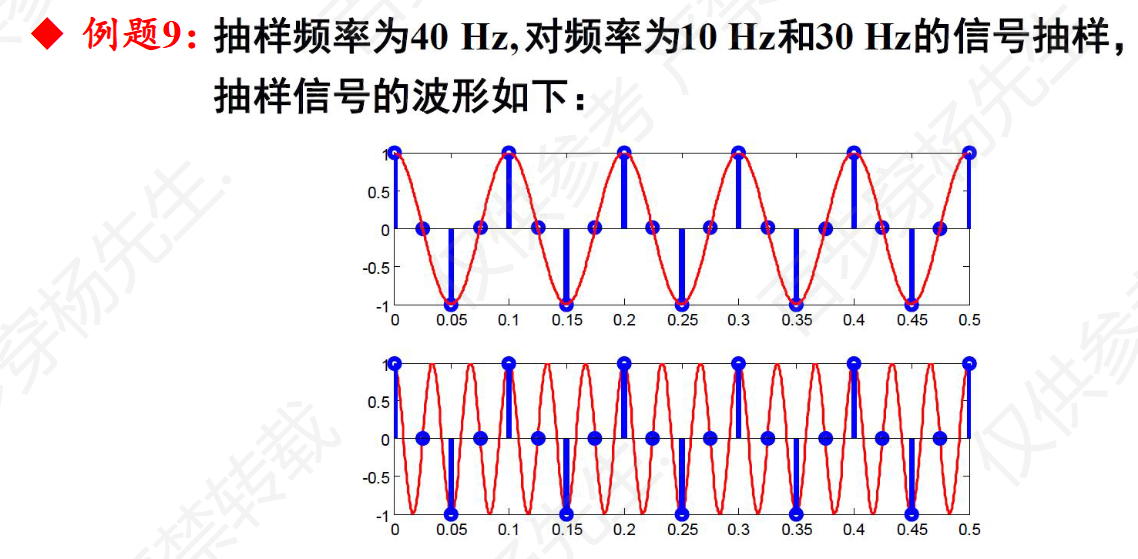
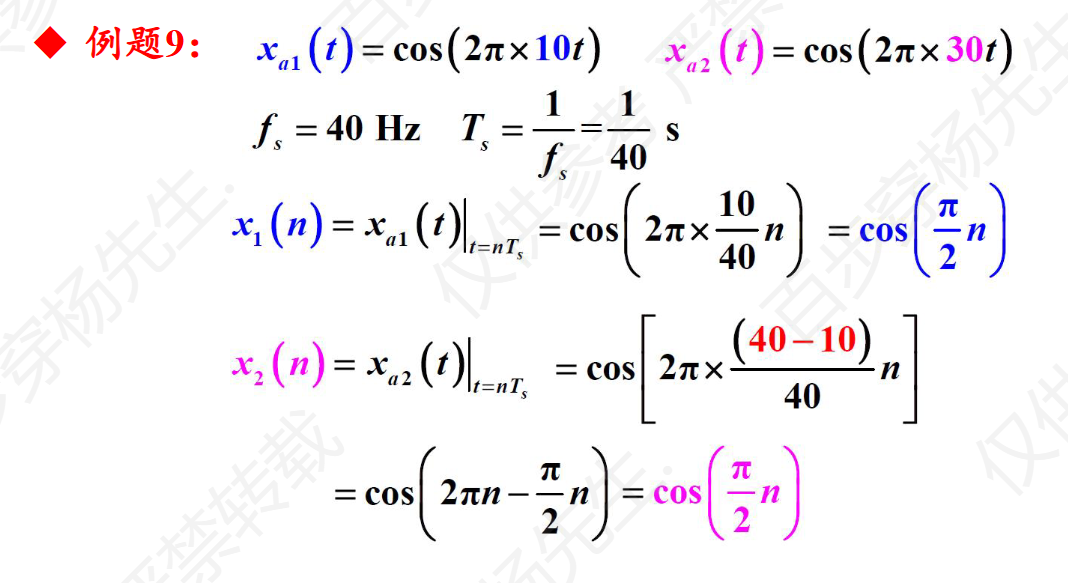
第五章计算题
例题1

例题2


例题3

例题4

例题5

例题6
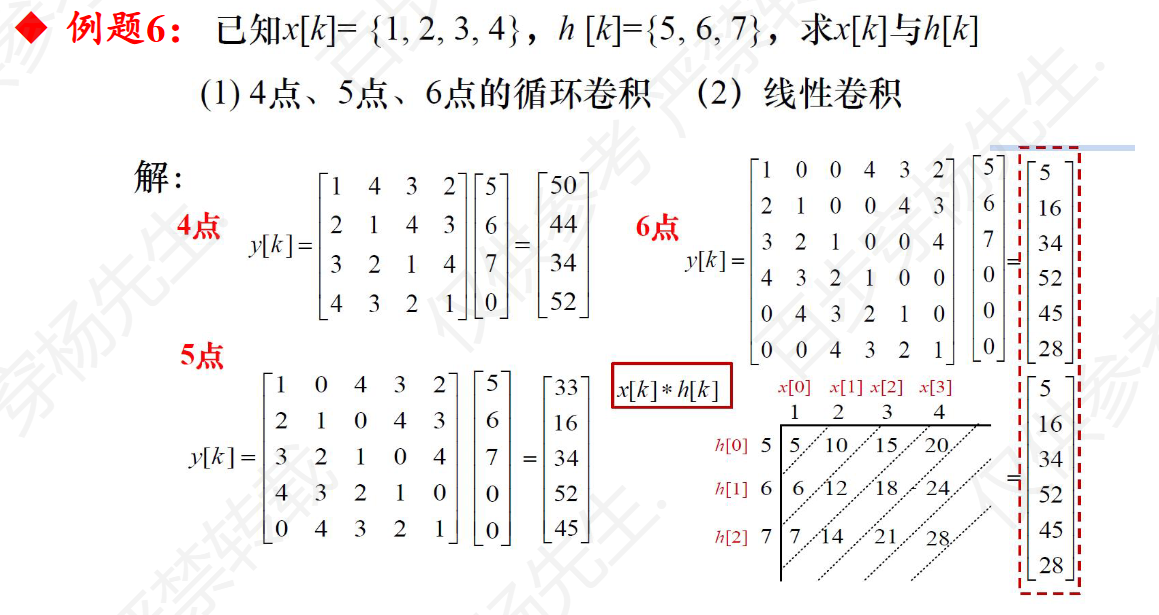
例题8

例题9 没理解

例题10
例题11

例题12

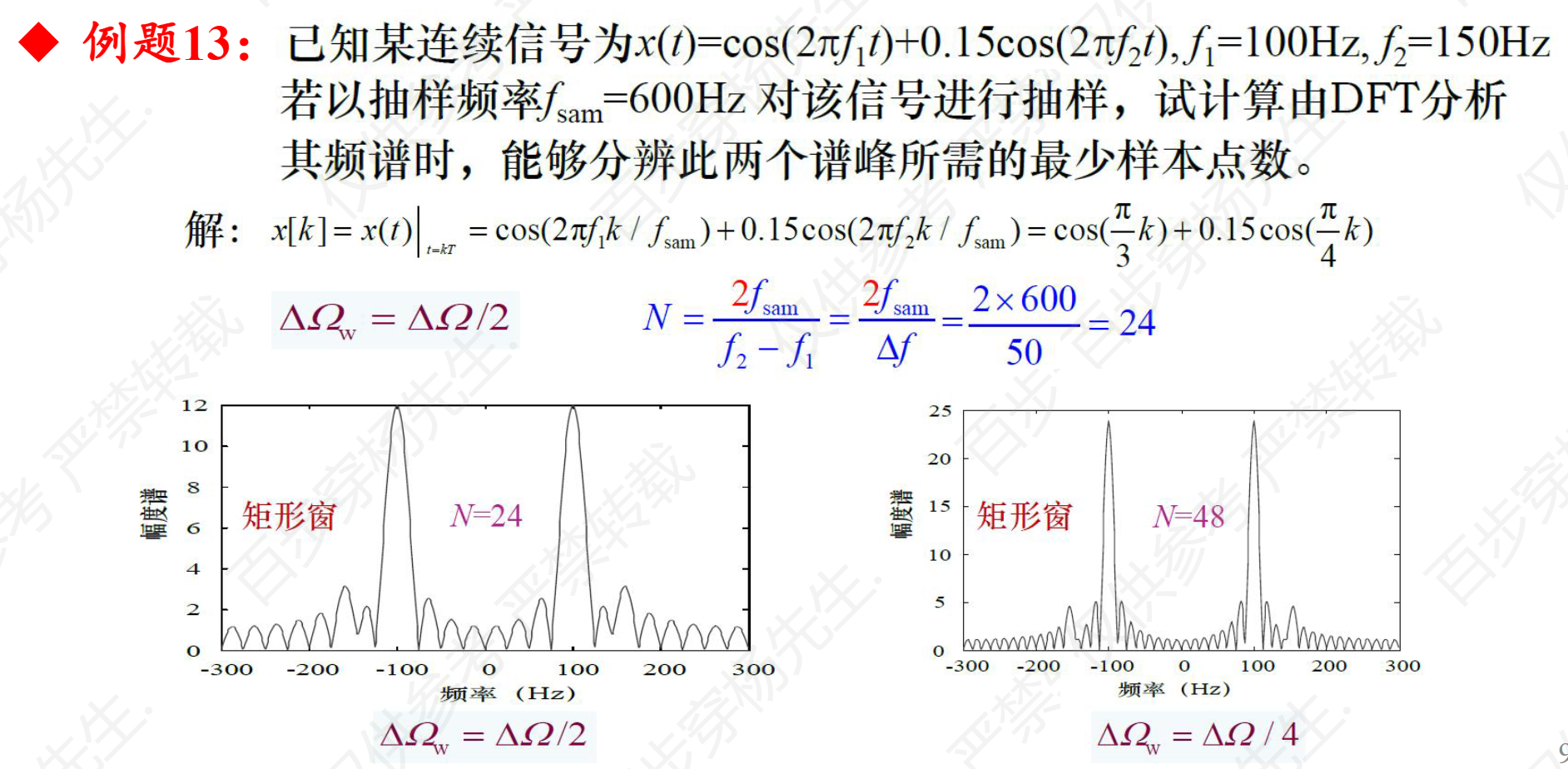
例题13
例题14

例题15

图像处理题

3、
图像增强 图像复原 图像形态学处理 图像分割 图像表示与表述 目标识别
5、

例题


卷积习题
习题1
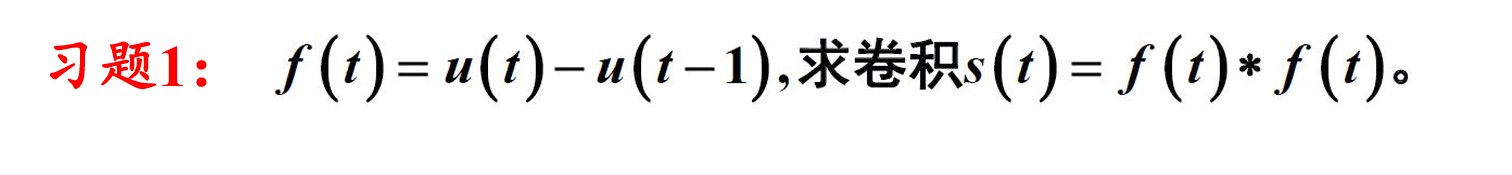
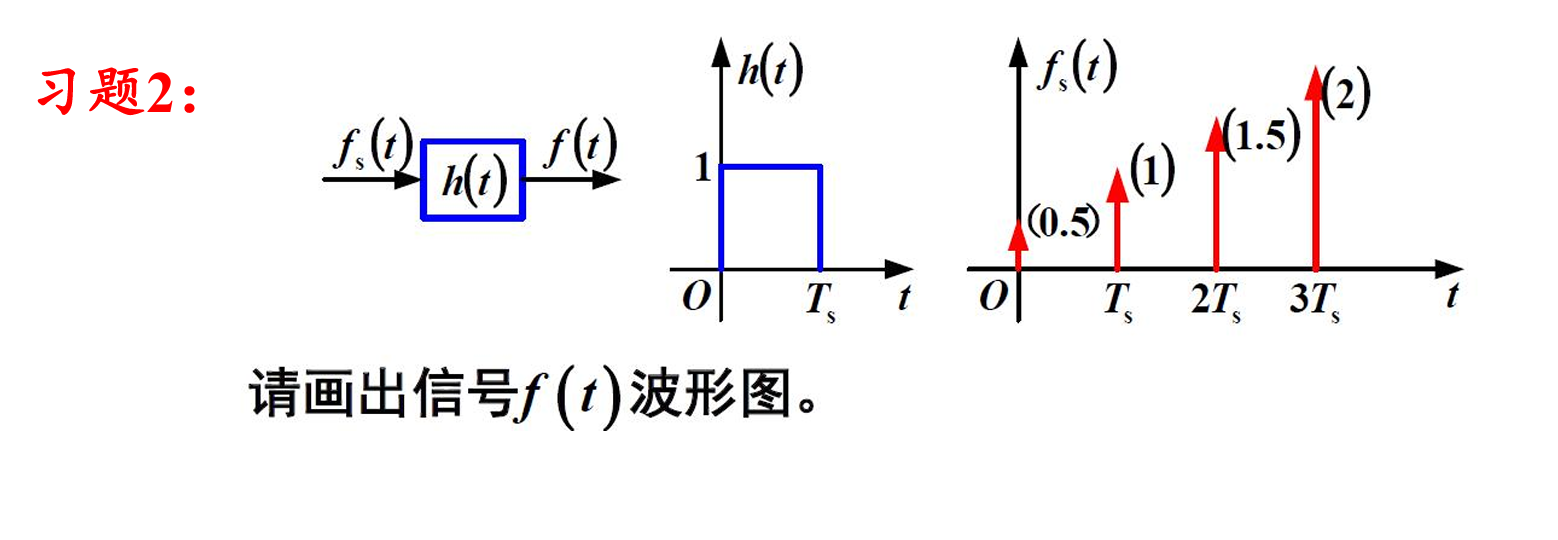
习题2 画图
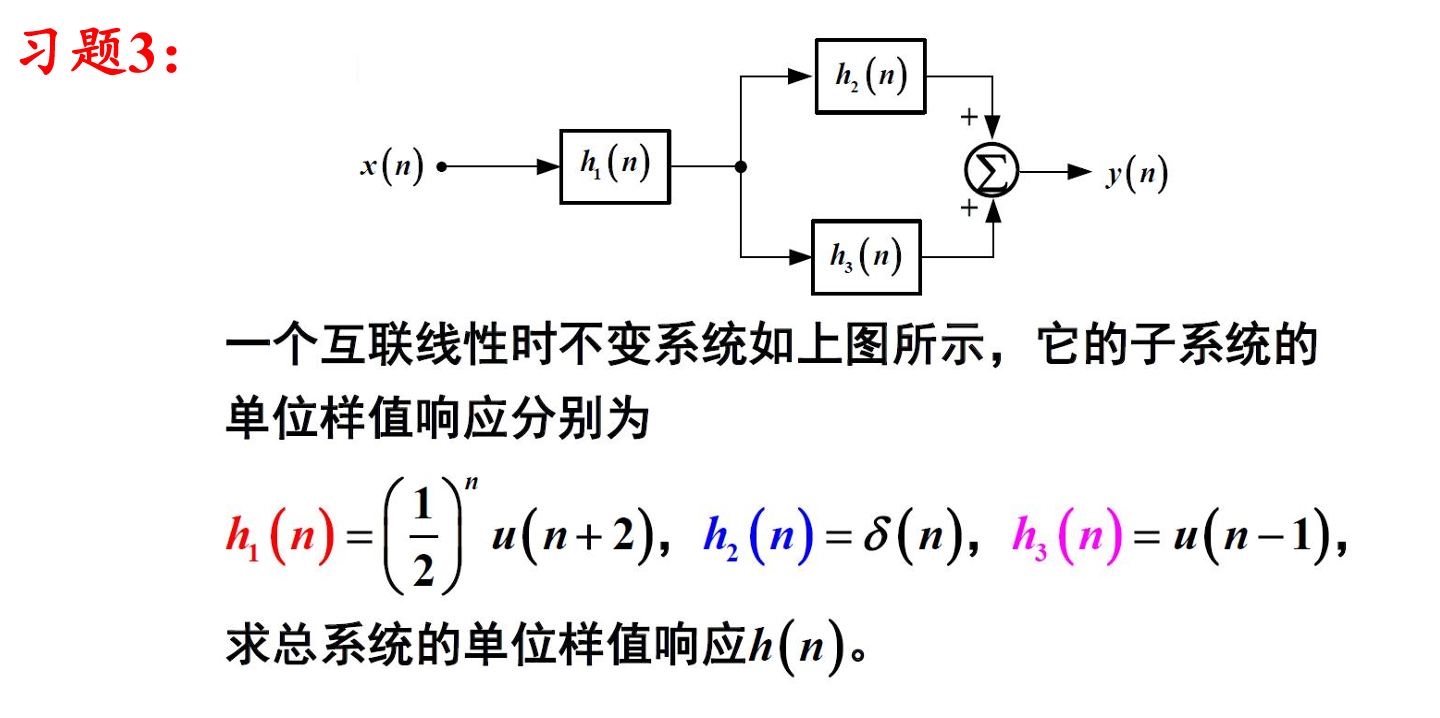
习题3
第三章习题
习题1

习题2
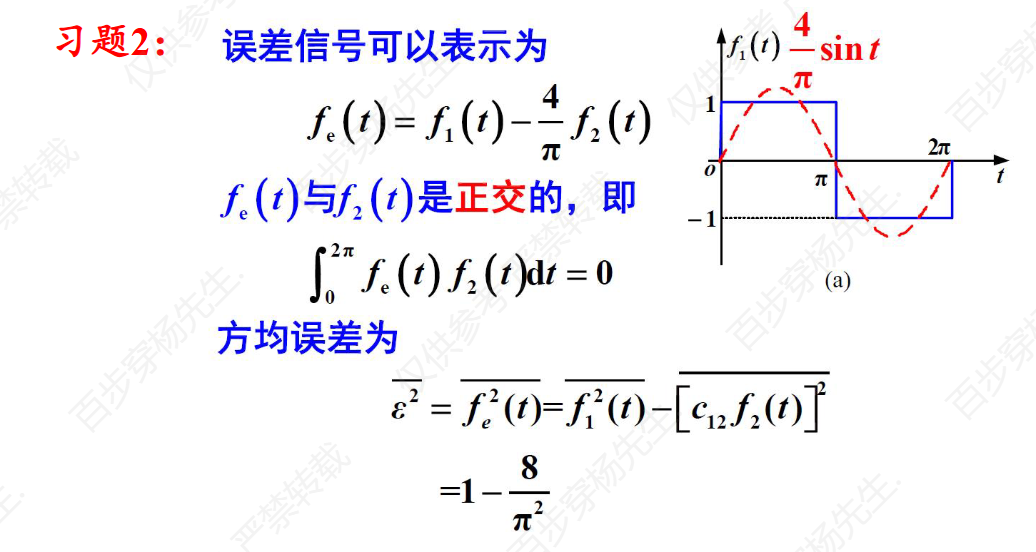
习题3

习题4

习题5

第四章习题
习题1 画图

习题2

习题3

第五章思考

1、理想低通滤波器是指在频率域中能够完全通过低频分量,同时完全阻止高频分量的滤波器
2、由于理想低通滤波器在实际应用中不可实现(其非因果性和时域无限响应),可以通过以下方式优化:
使用可实现的滤波器:
- 使用巴特沃斯滤波器或切比雪夫滤波器等接近理想低通特性的滤波器,频率响应平滑,且可实现。
减少 Gibbs 现象:
- 将理想低通滤波器的矩形响应替换为平滑的过渡函数,例如采用 Gaussian 滤波器。
调整窗函数:
- 设计有限时域的窗函数(如 Hamming 窗、Hanning 窗等)对信号进行加权,使频域响应更平滑,减少振铃效应。
频率调整:
- 根据信号实际需求选择合适的截止频率 fcf_cfc,避免过度滤波或不足滤波。
3、
低通滤波器: 允许低频分量通过,抑制高频分量,用于平滑信号或消除高频噪声。
高通滤波器: 允许高频分量通过,抑制低频分量,用于增强信号细节或边缘检测
- 高通滤波器可以看作低通滤波器的频域倒置版本。
4、
周期性噪声在频域中表现为孤立的频点:
- 空域: 周期性噪声是一种规则重复的波形,可能呈现为条纹、栅格等。
- 频域: 周期性噪声对应的频谱会在特定频率上产生孤立的高幅值频点,这些频点对应噪声的频率分量。
原因:
- 周期噪声是由特定频率的正弦波或余弦波叠加而成。在频域中,这些正弦波会集中在对应频率上形成孤立的频点。
5、
低通滤波器:
- Gaussian 滤波器: 平滑图像,减少噪声。
- Butterworth 滤波器: 平滑过渡,减少振铃效应。
- 理想低通滤波器: 理论滤波器,用于分析。
- 均值滤波器: 平均像素值,模糊图像,减少细节。
作用:
- 消除高频噪声。
- 平滑图像或信号。
- 保留大尺度的低频信息。
高通滤波器:
- Laplacian 滤波器: 检测图像的边缘。
- Sobel 滤波器: 强调边缘和轮廓。
- Butterworth 高通滤波器: 平滑过渡,抑制低频。
作用:
- 增强边缘或细节。
- 检测图像轮廓。
- 去除低频分量。
6、
低通滤波:
- 截止频率高: 保留更多高频细节,图像较清晰。
- 截止频率低: 仅保留低频分量,图像变得模糊。
高通滤波:
- 截止频率高: 仅增强非常高频的细节,图像边缘弱化。
- 截止频率低: 增强较多边缘信息,但可能带来噪声。
7、
图像的傅里叶变换:
- 将图像从空间域变换到频域,得到频谱表示(通常是复数形式)。
设计滤波器:
- 根据需求(低通、高通、带通或带阻)设计频率域滤波器。
滤波器与频谱相乘:
- 通过频域乘法实现滤波,将滤波器的频率响应应用于图像的频谱。
傅里叶逆变换:
- 对经过滤波的频谱进行傅里叶逆变换,返回空间域得到处理后的图像。
后处理:
- 对图像进行调整,例如归一化或去除噪声等。

作业题
复数表示
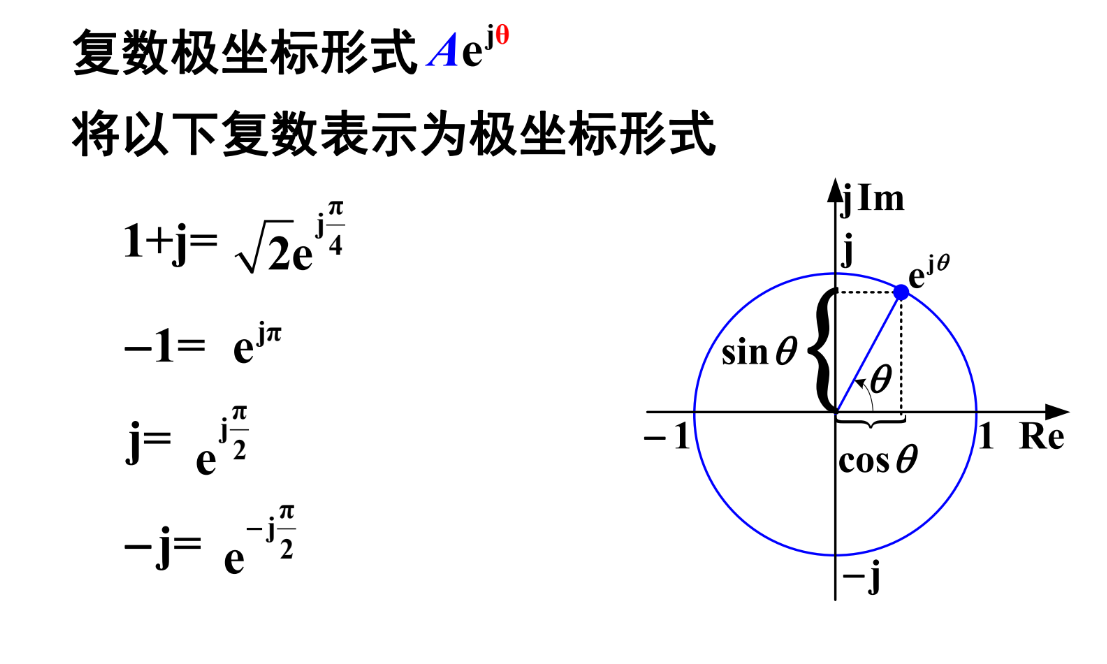
波形图绘制
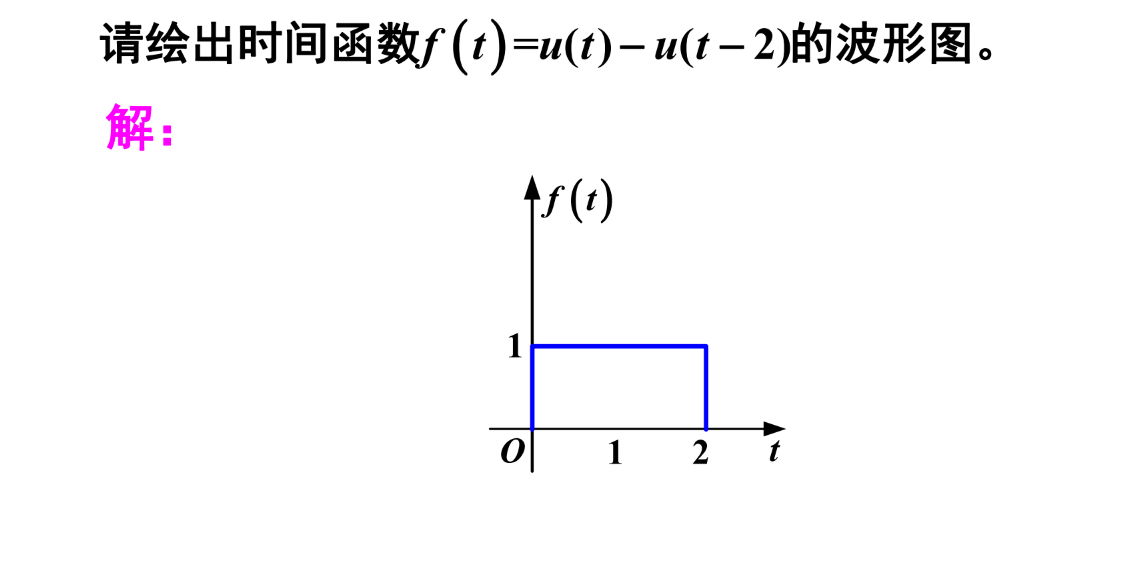
周期计算

平均功率

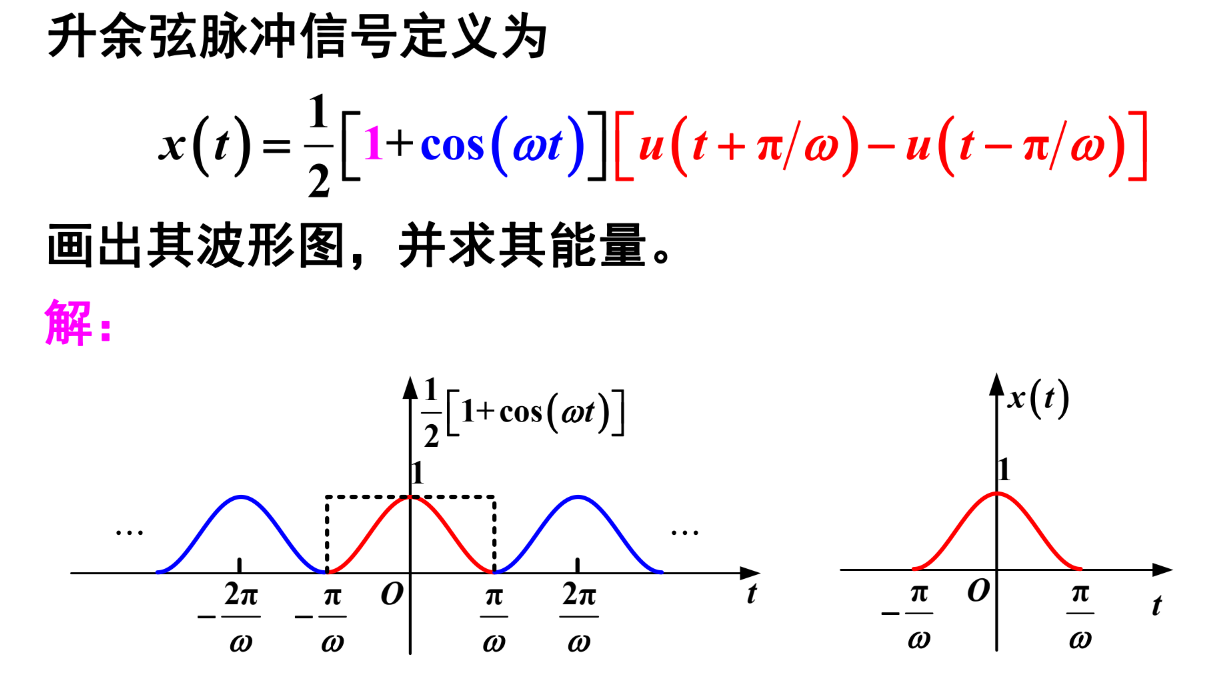
求能量
平移变换求函数
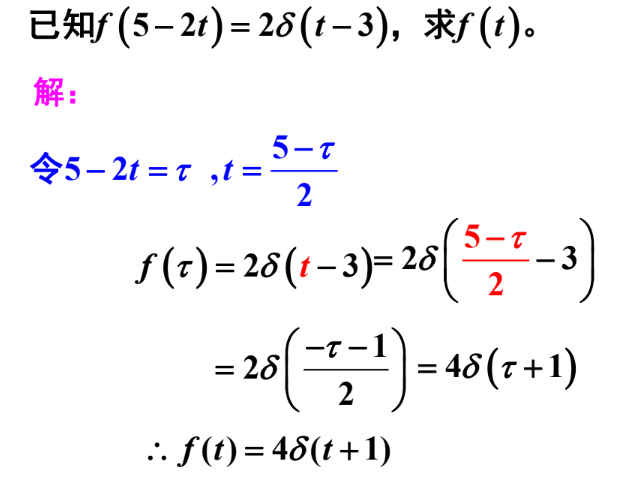
绘制波形图门函数

判断周期序列 *

确定基波周期

画出离散信号波形图
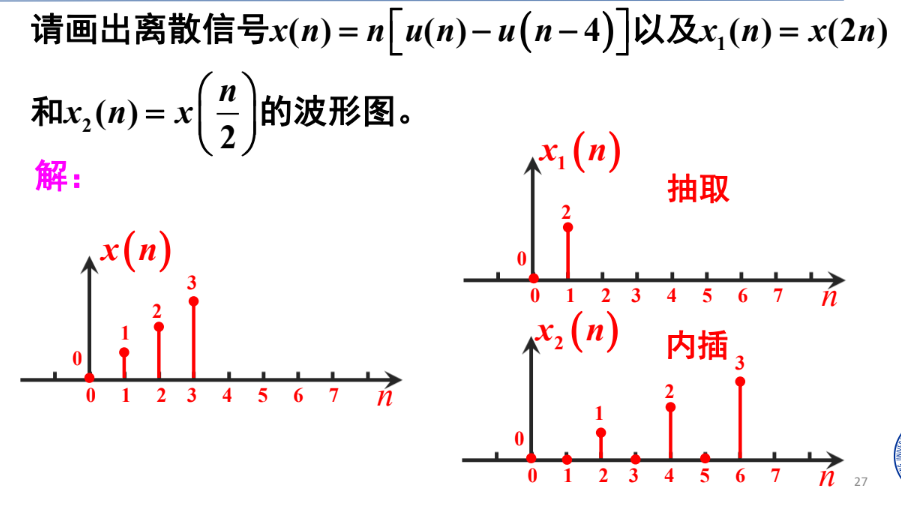

.png)

评论 (0)